Two identical particle 1 and 2 are projected from surface of earth with same velocity in the direction shown in figure.a Both the particle will stop momentarily at different timesb Particle -2 will rise upto lesser height compared to particle -2c Minimum speed of particle-2 is more than that of particle-1d Particle -1 will strike the ground earlier
Correct option b Particle -2 will rise upto lesser height compared to particle -2c Minimum speed of particle-2 is more than that of particle-1d Particle -1 will strike the ground earlierExplanation :1 will stop at minimum height while 2 will have a tangential velocity and particle 2 will rise lesser height than 1 as 2 do not looses its entire K.E. And particle 1 returns earlier.
Related Solutions
Assertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.
View SolutionAssertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.
View SolutionTwo identical particles and are projected from surface of earth with same velocities in the directions shows in figure.
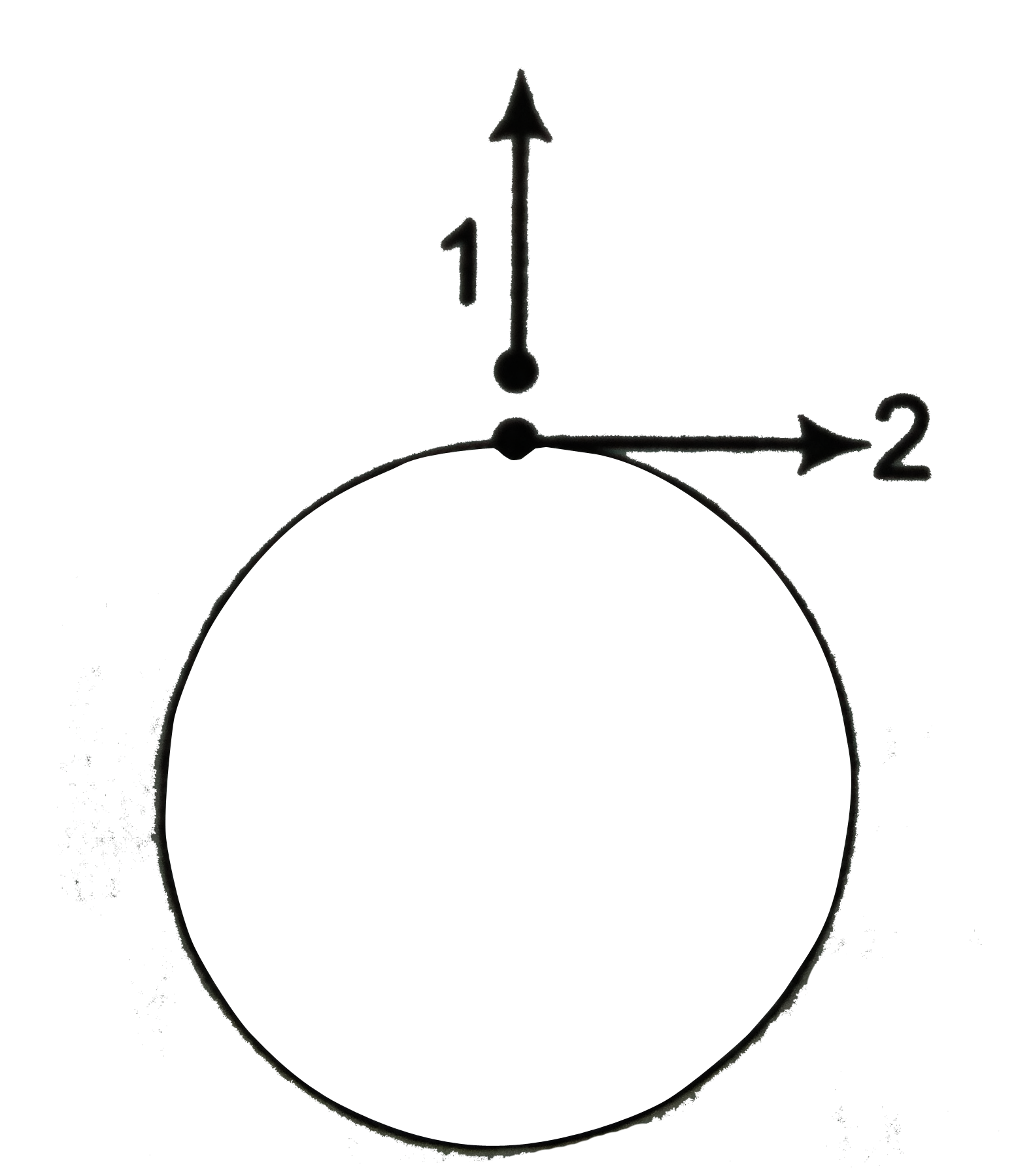
View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionA particle is projected from ground with speed u and at an angle with horizontal. If at maximum height from ground, the speed of particle is times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle is projected from ground with speed u and at an angle with horizontal. If at maximum height from ground, the speed of particle is times of its initial velocity of projection, then find its maximum height attained.
View SolutionTwo particles are projected from two high rise buildings simultaneously as shown then find minimum distance between particles.

View SolutionTwo particles are projected from two high rise buildings simultaneously as shown then find minimum distance between particles.

View SolutionTwo particles are projected from two high rise buildings simultaneously as shown then find minimum distance between particles.

View Solutionएक कण को पृथ्वी (त्रिज्या ) की सतह से ऊपर की ओर को ऊर्ध्वाधर दिशा में प्रक्षेपित किया जाता है | कण की गतिज ऊर्जा इसके पलायन के लिए आवशयक न्यूनतम ऊर्जा की आधी है | पृथ्वी की सतह से कण किस ऊँचाई तक जायेगा ?
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed (2v)/(sqrt(3)) . If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed (2v)/(sqrt(3)) . If particle B hits the particle A, the angle of projection of B with the vertical is
View Solutionदो कण A तथा B समान चाल से इस प्रकार प्रक्षेपित किए जाते हैं कि उनकी महत्तम ऊँचाईयों का अनुपात 3: 1 है। यदि कण A की चाल दोगुनी कर दी जाती है तब कण A तथा B की क्षैतिज परास का अनुपात होगा
View SolutionA particle is projected from the ground with a velocity of . After 2 sec, it just crosses a wall 10 m height. The angle of projection of the particle is
View SolutionA particle is released from a certain height H = 400m . Due to the wind, the particle gathers the horizontal velocity component v_x = ay "where a "= (sqrt5)s^(-1) and y is the vertical displacement of the particle from the point of release, then find (a) the horizontal drift of the particle when it strikes the ground , (b) the speed with which particle strikes the ground.
View SolutionA particle is released from a certain height H = 400m . Due to the wind, the particle gathers the horizontal velocity component v_x = ay "where a "= (sqrt5)s^(-1) and y is the vertical displacement of the particle from the point of release, then find (a) the horizontal drift of the particle when it strikes the ground , (b) the speed with which particle strikes the ground.
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The time of flight of that particle is
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The range of that particle is
View SolutionTwo particles of equal mass 'm' are projected from the ground with speed and at angles and at the same times as shown in figure. The centre of mass of the two particles.

View SolutionTwo particles of equal mass 'm' are projected from the ground with speed v_(1) and v_(2) at angles theta_(1) and theta_(2) at the same times as shown in figure. The centre of mass of the two particles.
View Solution