Two interacting particles form a closed system whose centre of inertia is at rest. Fig. 1.36 illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass m1. Draw the trajectory of the particle of mass m2 if m2 = m1/2.
As the closed system consisting two particles m1 and of m2 is initially at rest the C.M. of the system will remain at rest. Further as m2 = m1/2 the C.M. of the system divides the line joining m1 and m2 at all the moments of time in the ratio 1: 2. In addition to it the total linear momentum of the system at all the times is zero. So vector P1=-vector P2 and therefore the velocities of m and m are also directed in opposite sense. Bearing in mind all these thing the sought trajectory is as shown in the figure.
Related Solutions
Two interacting particles form a closed system whose centre of mass is at rest. Fig. illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass . Select the trajectory of the particle of mass if .

View SolutionTwo interacting particles from a closed system whose centre of inertia is at rest. Figure illustrates the positions of both particles at a certain moment and the trajectory of the particle of mass m_2 . Draw the trajectory of the particle of mass m_2 if m_2=m_1//2 .
View SolutionA stationary particle explodes into two particle of masses m1 and m2 and move in opposite directions with velocities v1 and v2.The ratio of their K.E is
View SolutionDefine gravitational potential energy and derive an expression for it associated with two particles of masses m1 and m2.
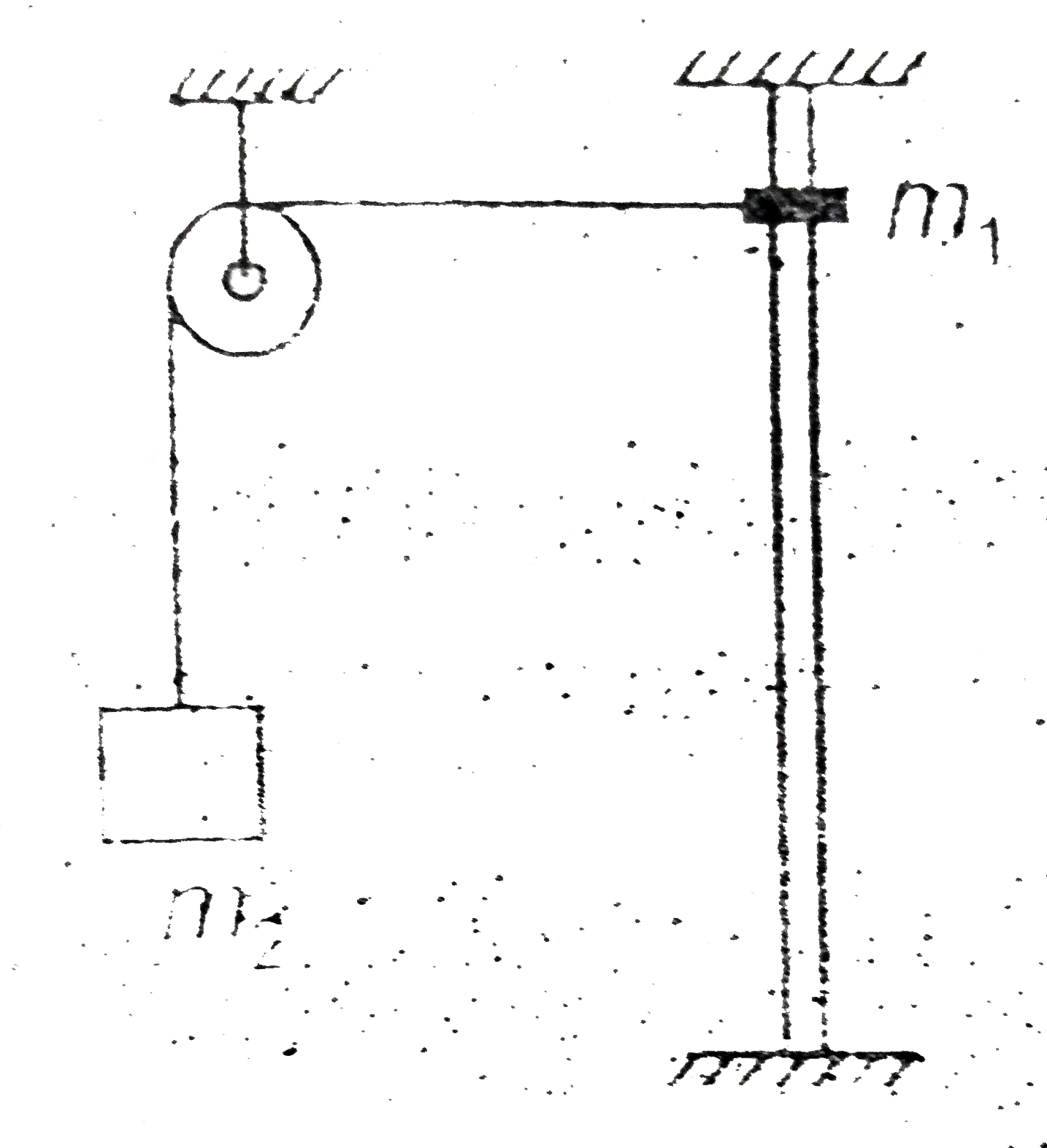
View SolutionA smooth ring of mass connected with a hanging block of mass by a long inextensible string, is released from rest. The ring moves vertically along a fixed rigid rod as shown in figure. Describe the motion of the ring if
(A)
(B)
(C )
View SolutionTwo masses m1 and m2 are connected by light string, which passes over the top of a smooth plane inclined at 30º to the horizontal, so that one mass rests on the plane and the other hangs vertically as shown in fig. It is found that m1, hanging vertically can draw m2 up the full length of the plane in half the time in which m2 hanging vertically draws m1 up. Find m1/m2 . Assume pulley to be smooth-

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionDiscuss different cases, to find final velocities for two bodies in the below expression for v_(1f)=((m1-m2)v1i)/(m1+m2) and v_(2f)=(2m1v1i)/(m1+m2)
View SolutionA rigid body consists of particles of mass ,,,........... The body rotates about an axis with an angular velocity
Starting from kinetic the energy of a single particle,arrive at an equation of kinetic energy of rotation.
View SolutionFigure shows the initial position of a system of two particles. Given that centre of mass of the system remains at rest particle moves i a trajectory givenn by
Pick the correct option (s) for the nature of trajectory and the coordinates of at the instant when was at the position .

View SolutionFigure shows the initial position of a system of two particles. Given that centre of mass of the system remains at rest particle moves i a trajectory givenn by
Pick the correct option (s) for the nature of trajectory and the coordinates of at the instant when was at the position .

View SolutionA partical of mass m1 is travelling with avelocity u1 strikes head-on against partical of mass m2 at rest.After collision the particales move with a velocity v1 and v2 respectively .show that the ratio of decrese in K.E of the partical of mass m1 to its original K.E is given By (4m1m2)/(m1+m2)^2
View Solutionf(x)=|x-1|+|x-2|,g(x)=x+(1)/(x),x>0* if m 1=min(f(x)) and m2=min(g(x)) then (m2+m1)/(m2-m1) is equal to
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2 . Find the time period and amplitude of resultant motion. (Given : spring constant is K.)
View SolutionThe position of centre of mass of system of particles at any moment does not depend on.
View SolutionThe position of center of mass of a system of particles does not depend upon the
View SolutionThe centre of mass of the system of particles depends on
(a) masses of the particles
(b) Relative position of the particles
View SolutionThe centre of mass of the system of particles depends on (a) masses of the particles (b) Relative position of the particles
View Solution