A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals vo and forms an angle α with the horizontal.
The force with which the cylinder wall acts on the particle will provide centripetal force necessary for the motion of the particle and since there is no acceleration acting in the horizontal direction horizontal components of the velocity will remain constant throughout the motion.
Related Solutions
A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals and forms an angle with the horizontal.
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v_(0) . And forms an angle alpha with the horizontal.
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v_(0) . And forms an angle alpha with the horizontal.
View SolutionA particle of mass m moves along the inner smooth surface of a vertical cylinder of radius R. If at the initial instant of time, the velocity of the particle v_0 is equal to, and it is an angle with the horizontal alpha Find the force with which the particle acts on the wall of the cylinder.
View SolutionA particle of mass m and velocity v_(0) is fired at a solid cylinder of mass M and radius R. The cylinder is initially at rest and is mounted on a fixed horizontal axle that runs through the centre of mass. The line of motion of the particle is perpendicular to the axle and at a distance d, less than R, from the centre and the particle sticks to the surface of the cylinder, then
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionTo keep a particle moving with constant velocity on a frictionless surface, an external force .
View SolutionA particle moves from rest at A on the surface of a smooth circular cylinder of radius r as shown. At B it leaves the cylinder. Find the value of (4cos alpha)/(3sinbeta)
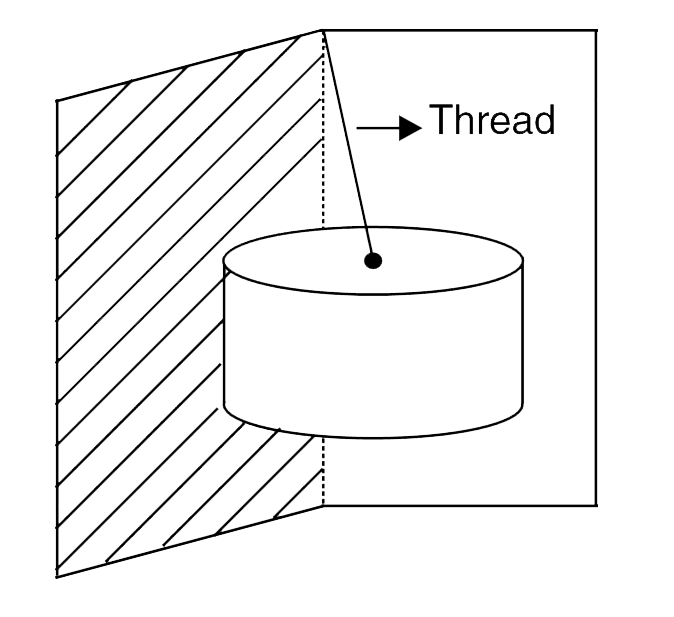
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View SolutionA cylinder of mass M and radius r is suspended at the corner of a room. Length of the thread is twice the radius of the cylinder. Find the tension in the thread and normal force applied by each wall on the cylinder assuming the walls to be smooth.
View SolutionA particle of mass m moves along a circle of radius R. Find the modulus of the average vector of the force acting on the particle over the distance equal to a quarter of the circle, if the particle moves (a) uniformly with velocity v , (b) with constant tangential acceleration w_tau , the initial velocity being equal to zero.
View SolutionA solid cylinder of mass 'M' and radius 'R' is rotating along its axis with angular velocity omega without friction. A particle of mass 'm' moving with velocity v collides aganist the cylinder and sticks to its rim. After the impact calculate angular velocity of cylinder .
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance (R)/(2) from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
View SolutionA particle of mass is projected with velocity at an angle with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is .
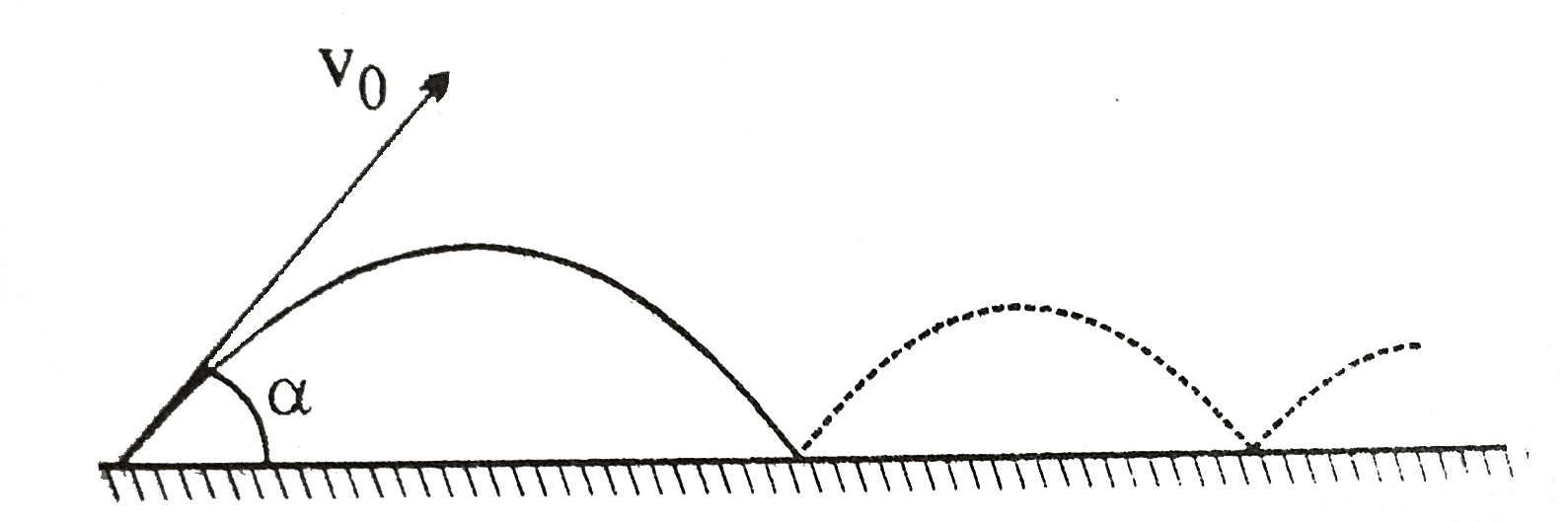
Find total time taken by the particle before it stops moving vertically?
View SolutionA particle of mass 'm' is projected with velocity v_(0) at an angle 'alpha' with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is e . Find total time taken by the particle before it stops moving vertically?
View SolutionA particle of mass m moves along a circle of radius 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is:
View SolutionA hollow vertical cylinder of radius R and height h has a smooth inner surface. A small particle is placed at a point P in contact with the inner surface of the upper routine. It is given the tangential horizontal speed Vo of the routine. It bypasses the lower routine at point Q which is vertically below P. The number of revolutions made by the particle will be:
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Velocity of point of contact 'of cylinder at this moment is:
View Solution