Figure shows two arcs PAQ and PBQ and PAQ is a part of circle with centre O and radius OP while are PBQ is a semi-circle drawn on PQ as diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is 25√3 -π /6 cm2.
OP = OQ = PQ = 10 cm
Related Solutions
In the given figure, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while are PBQ is a semi-circle drawn on PQ as diameter with centre M. OP=PQ=10 cm show that area of shaded region is 25(sqrt3-pi/6) cm^2
View SolutionIn the given figure,are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while are PBQ is a semi-circle drawn on PQ as diameter with centre M.If PQ=OP=10cm show that area of shaded region is 25(sqrt(3)-(pi)/(6))
View Solutionआकृति में , दो चाप PAQ तथा PBQ दर्शाए गए है चाप PAQ ,O केन्द्र वाले वृत का भाग है , जिसकी OP है तथा चाप PBQ ,PQ का व्यास मानकर बनाया गया अर्द्धवृत है जिसका केन्द्र M है यदि OP =PQ = 10 सेमी है तो दर्शाइए की भाग का क्षेत्रफल सेमीहै |
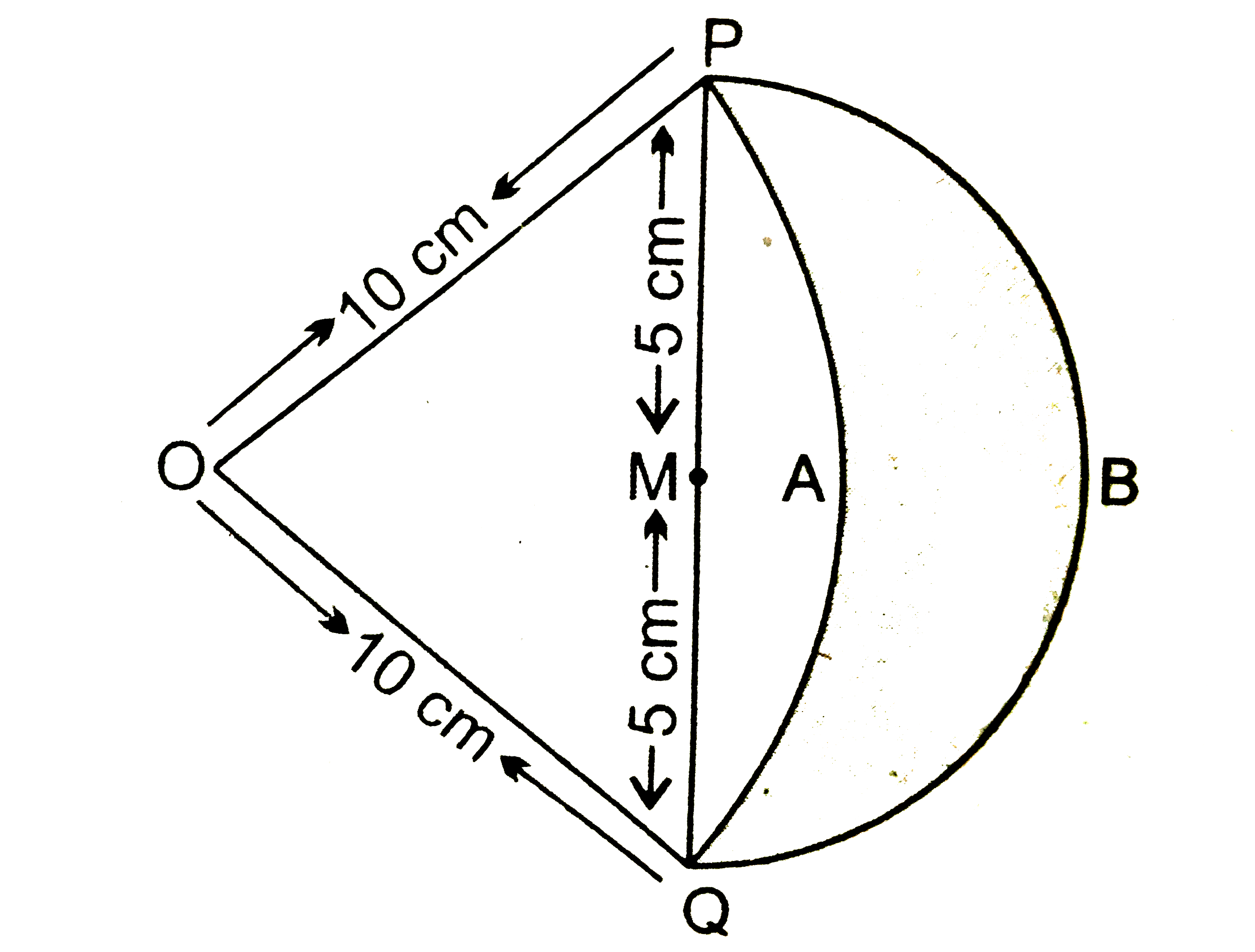
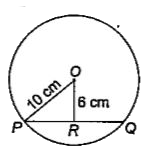
View SolutionIn a given figure, a circle with centre O. Radius of circle is OP = 10 cm and chord PQ on which OR = 6 cm is perpendicular, length of PQ is
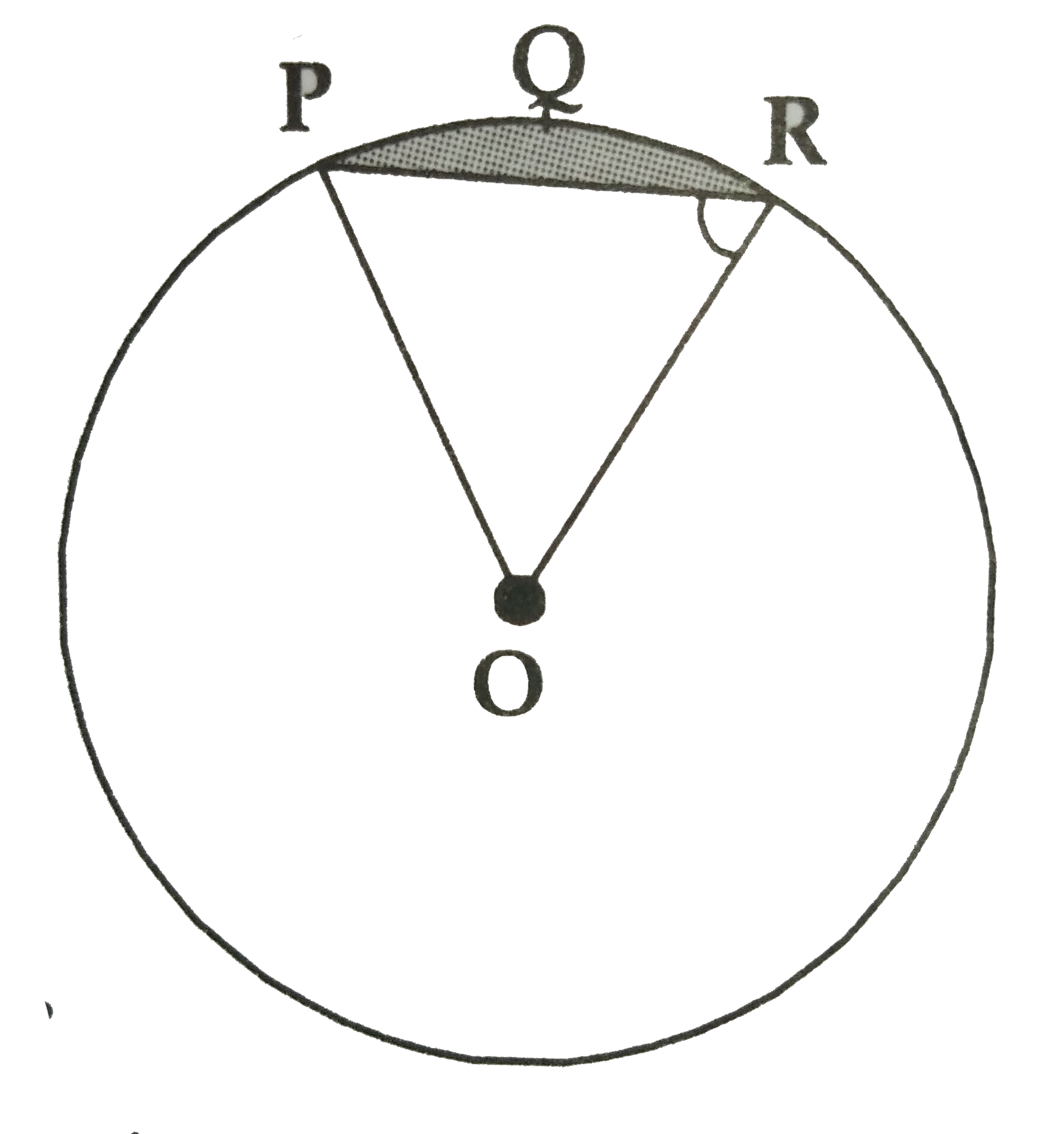
View SolutionIn the figure, O is the centre of the circle.
m(arc PQR)
OP = 10 cm.
Find the area of the shaded region.

View SolutionCircle inside a Circle : PQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal. Semi circles are drawn on PQ and QS as diameters, as shown in Figure. Find the perimeter and area of shaded Region.
View SolutionThe diagram shown two arcs, A and B. Arc A is part of the circle with centre and radius . Arc is part of the circle with centre and radius , where is the mid-point of PQ. Show that the area enclosed by the two arcs is equal to
View SolutionPQRS is the diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn with PQ and QS as diameters as shown in the figure alongside. Find the ratio of the area of the shaded region to that of the unshaded region.
View SolutionThe chord PQ is the perpendicular bisector of the radius OA of the circle with center O (A is the point on the circle). If arc PAQ = (2pi)/3 Then what is the length of the chord PQ?
View SolutionIn the adjoining figure, O is the centre of the circle.
m(arc PQR) OP=10 cm
Find the area of the shaded region.
Given
To find: A(shaded region)
View Solutionएक वृत्त का केन्द्र O तथा त्रिज्या OP = 10 सेमी है। जीवा PQ की लम्ब OR की लम्बाई 6 सेमी है। तब PQ का मान ज्ञात कीजिए।
View SolutionChord is the perpendicular bisector of radius OA of circle with centre O (A is a point on the edge of the circle). If the length of Arc . What is the length of chord ?
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionFind the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
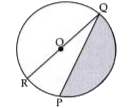
View SolutionFind the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
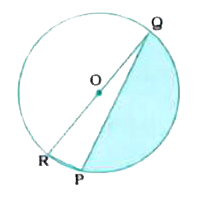
View SolutionFind the area of the segments shaded in figure, if PQ = 28 cm, PR = 8 cm and QR is the diameter of the circle with centre O.
View SolutionPQRS is a diameter of a circle of radius 6 cm as shown in the figure above. The lengths PQ, QR and RS are equal. Semi-circles are drawn on PQ and QS as diameters. What is the perimeter of the shaded region ?
View SolutionPS is a diameter of a circle of radius 6 cm. In the diameter PS, Q and R are two points such that PQ, QR and RS are all equal. Semi-circles are drawn on PQ and QS as diameter (as shown in the figure). The perimeter of shaded portion is :
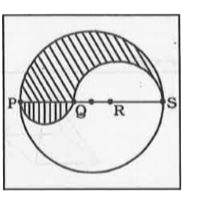
View SolutionIn the figure, if O is the centre of the circle, PQ is chord. area of shaded region is find the radius of the circle
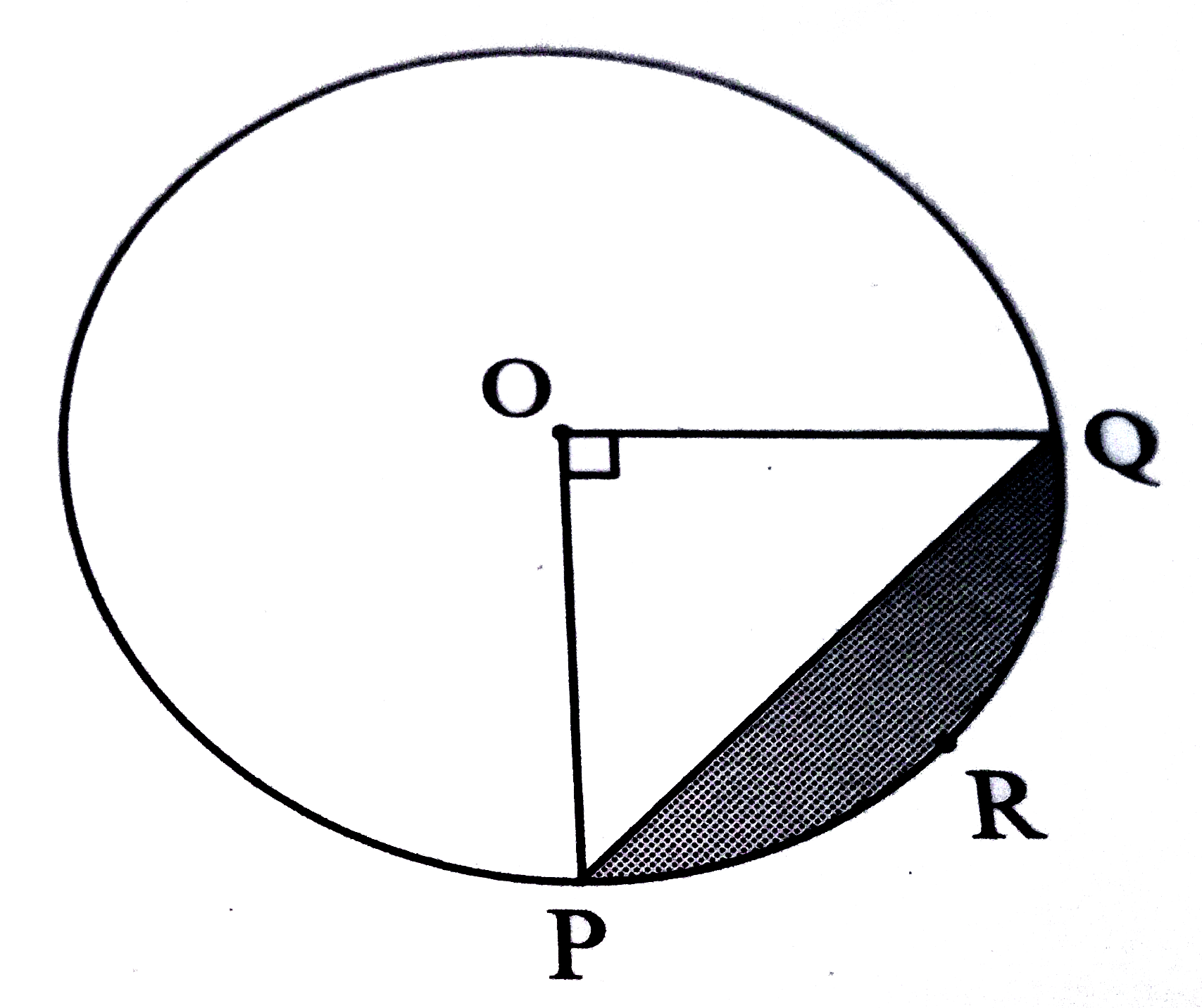
View Solution