In a circle point P is its center and PA = PB = radius of the circle. Where do points A and B lie ?
A circle is given with center P and PA = PB = radius of the circle.∵ The radii of a circle are equal there they lie on the circumference of the circle In other words the path of a point which is equidistant from a fixed point is the circumference of a circle. The fixed point is called the center and equidistance is the radius.
Related Solutions
A point P moves such that PA/PB = p where A and B are two fixed pints with AB=a, the locus of P is a circle with radius
View SolutionPA and PB are two tangents drawn from an external point P to a circle with center O where points A and B are the points of touch. The quadrilateral OAPB must be-
View SolutionO is the centre of a circle. There is a point P in the region of the circle. If PA = PB = PC where A, B and C are points on the circumference of the circle, then OP must be equal to :
View SolutionPA and PB are tangents from a point P outside a circle with O center. A and B are any two points on the circle. If angleAPB = 72^(@) So angleOAB Is equal:
View SolutionPA and PB are tangents to a point P outside a circle with center O and A and B. are two points on the circle. If angleAPB= 30^(@) is, then angleOAB Is equal:
View SolutionPA and PB are tangents to a point P outside a circle with center O and A and B are two points on the circle. If angleAPB= 40^(@) is, then angleOAB Is equal.
View Solutionयदि बिन्दु P से वृत्त पर खींची गई दोनों स्पर्शियो PA और PB की समान लम्बाई 4 सेमी है, तो वृत्त की त्रिज्या है :
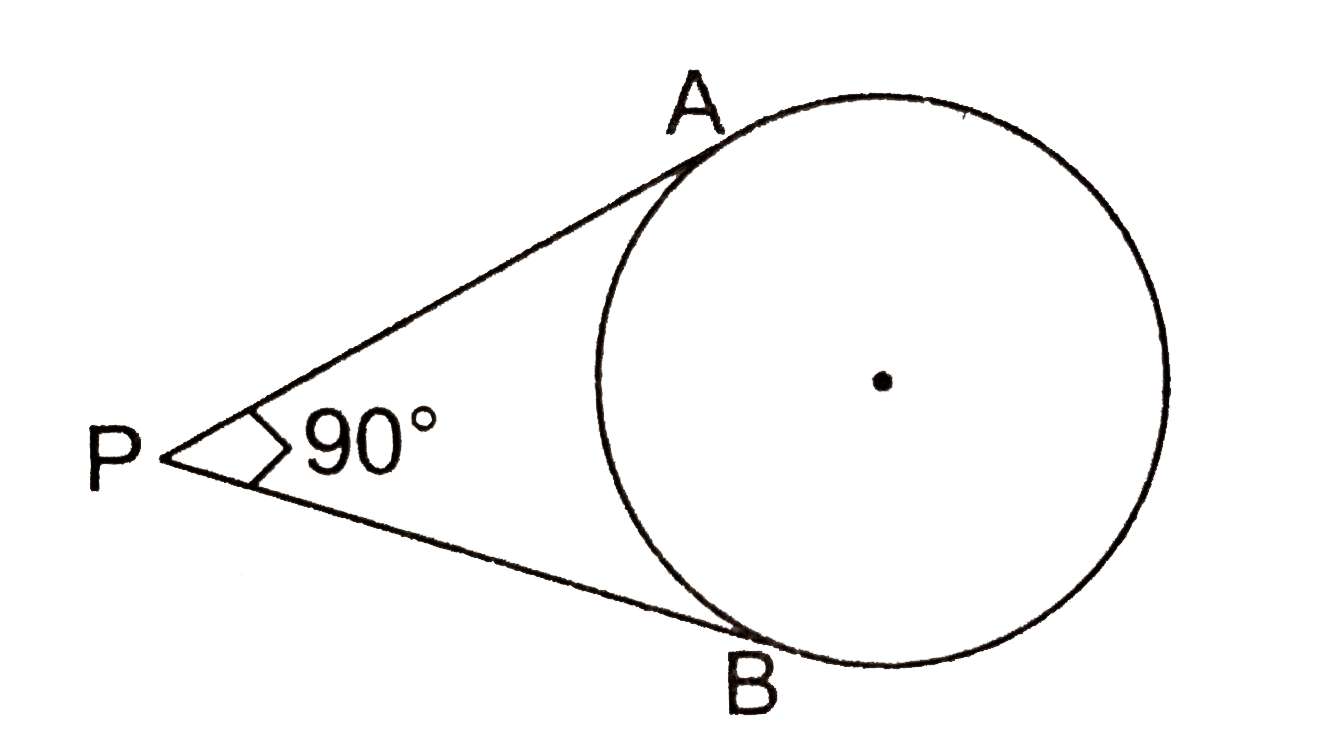
View Solutionयदि एक बिंदु P से O केंद्र वाले वृत्त पर PA , PB स्पर्श रेखाएँ परस्पर के कोण पर झुकी हों, तो बराबर है :
View SolutionThere is a point P outside a circle, which is 26 cm from the center of the circle. Is at a distance of. An intersection line drawn from P to PAB cuts the circle at points A and B such that PB = 32 cm, and PA = 18 cm. Lets do it. Find the radius (in cm) of the circle.
View SolutionP is a point outside a circle and is 26cm away from its centre.A secant PAB drawn from intersects the circle at points A and B such that PB = 32 cm and PA = 18 cm. The radius of the circle ( in cm ) is
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If angle PAB = 47^(@) , then angle OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If , then is equal to:
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If , then is equal to
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If , then OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If angleAPB= 70^@ then angleOAB is equal to:
View SolutionPA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If , then is equal to:
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View SolutionFrom an external point P to a circle with center O, two tangents PA and PB are drawn to the circle and meet the circle at points A and B. If angleAPB= 70^(@) So angleOAB The value of.
View SolutionPA and PB are the two tangents drawn to a circle centered at o. from an external point P . If = then is
View SolutionPA and PB are two tangents drawn to a circle with center O from an external point P. If = …….
View Solution