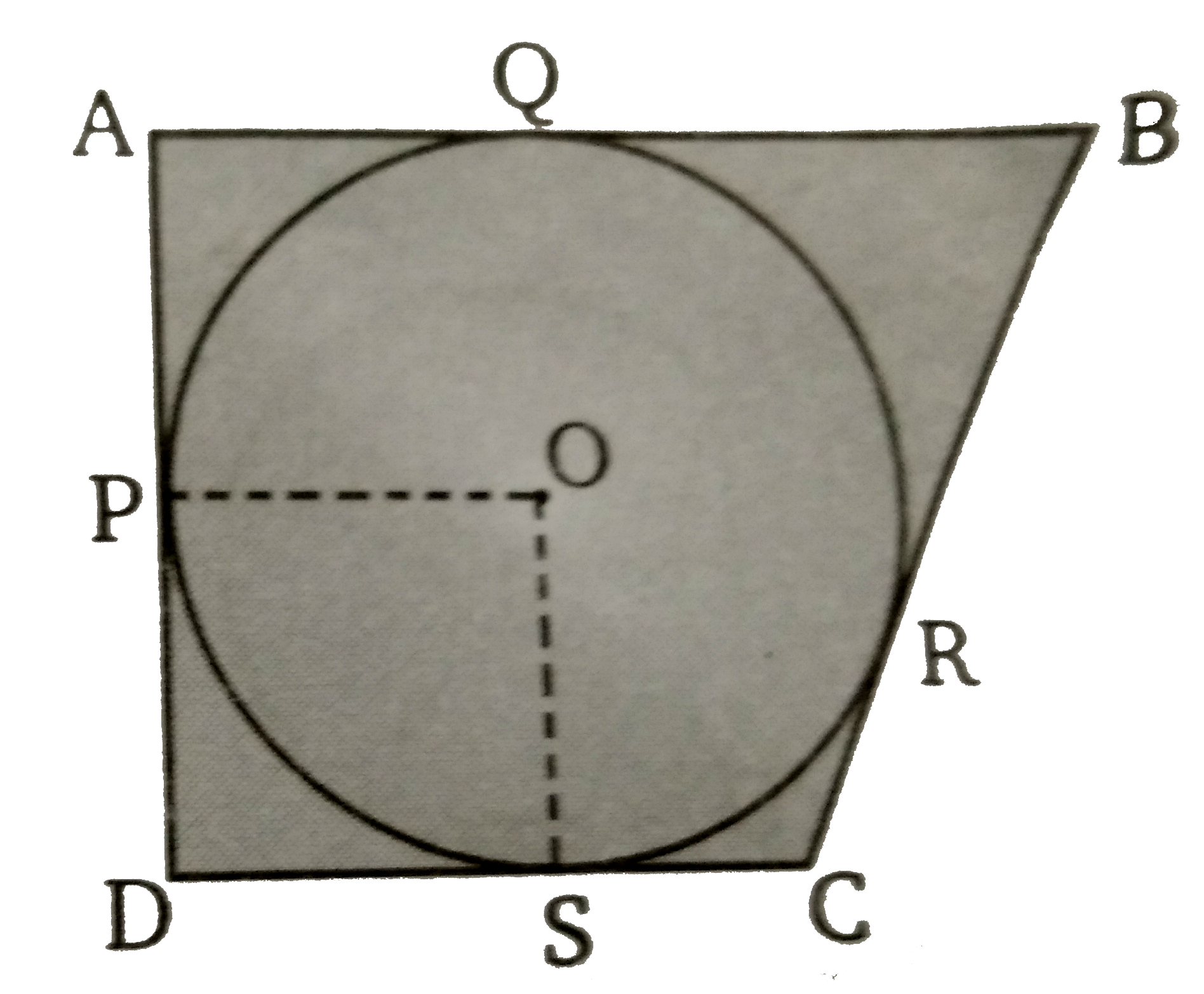
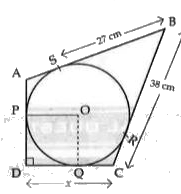
In the following figure a circle is inscribed in the quadrilateral ABCD.If BC = 38 cm QB = 27 cm DC = 25 cm and that AD is perpendicular to DC find the radius of the circle.
From the figure we see that BQ = BR = 27 cm since length of the tangent segments from an external point are equalAs BC = 38 cmCR = CB − BR = 38 − 27= 11 cmAgain CR = CS = 11cm length of tangent segments from an external point are equalNow as DC = 25 cm∴ DS = DC − SC= 25 − 11= 14 cmNow in quadrilateral DSOP ∠PDS = 90° given∠OSD = 90° ∠OPD = 90° since tangent is perpendicular to the radius through the point of contactDSOP is a parallelogramOP ∥ SD and PD ∥ OSNow as OP = OS radii of the same circleOPDS is a square. ∴ DS = OP = 14cm∴ radius of the circle = 14 cm
Related Solutions
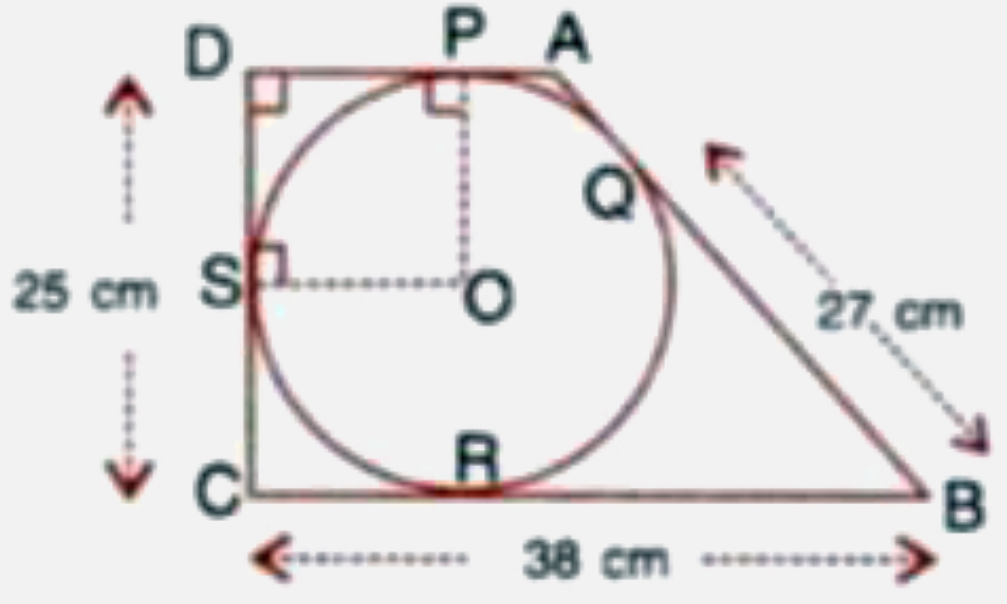
In the above figure there is an incircle in the quadrilateral ABCD. BC = 38 cm, QB = 27 cm, DC = 25 cm and AD, is perpendicular to DC. What is the radius of the circle?
View SolutionIn the adjacent figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and AD is perpendicular to DC then what is the radius of the circle ?
View SolutionIn the above figure there is an incircle in quadrilateral ABCD. BC = 38 cm, QB = 27 cm, DC = 25 cm and AD _|_ DC. What is the radius of the circle?
View Solutionएक चतुर्भुज ABCD (चित्र) के अन्दर एक वृत्त इस प्रकार है कि BC = 38 सेमी, BQ = 27 सेमी, DC = 25 सेमी तथा AD, DC पर लम्ब है। वृत्त की त्रिज्या ज्ञात कीजिए ।
View SolutionIn the following figure, a circle is inscribed in th equadrilaterial ABCD.
 width="80%">
width="80%">
If BC=38 cm, QB=27cm, DC=25 cm and that AD is perpendicular to DC, find the radius of the circle.
View SolutionIn quadrilateral ABCD, angle ,dc=25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27 cm. Find the radius of the circle.
View SolutionA circle is inscribed in the quadrilateral ABCD. Given BC= 38 cm . BQ= 27 cm , CD = 25 cm and angleADC = 90^(@) find the radius of the circle .
View SolutionIn the figure
Find the radius of the circle.
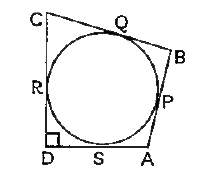
View SolutionIn the given figure, a circle inscribed in a quadrilateral ABCD touches its sides AB, BC CD and AD at P, Q, R and S respectively. If radius of circle is 10 cm, BC = 38 cm, PB = 27 cm and AD bot CD then find the length of CD.
View SolutionIn the figure, ,
. Find the radius of the circle.
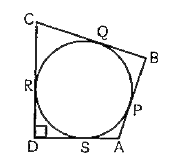
View SolutionIn the adjoining figure, quadrilateral ABCD is circumscribed. If the radius of the incircle with centre O is 10 cm and AD is perpendicular to DC, find x.
View SolutionA circle of radius 4 cm is inscribed in DeltaABC , which touches side BC at D. If BD = 6 cm, DC = 8 cm then
View SolutionA circle of radius 4 cm is inscribed in , which touches side BC at D. If BD = 6 cm, DC = 8 cm then
View SolutionA circle of radius 4 cm is inscribed in AABC, which touches the side BC at D. If BD = 6 cm, DC = 8 cm, then
View SolutionA circle of radius 4 cm is inscribed in , which touches side BC at D. If BD = 6 cm, DC = 8 cm then
View SolutionA circle of radius 4 cm is inscribed in , which touches side BC at D. If BD = 6 cm, DC = 8 cm then
View SolutionABCD is a quadrilateral such that . A circle C of radius r touches the sides AB, BC, CD and DA at P, Q, R and S respectively. If BC = 38 cm, CD = 25 cm and BP = 27 cm. Find r
View SolutionIn quadrilateral ABCD angled , BC=38cm and DC=25cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27cm. Find the radius of the circle.
View Solution/_\ABC AD perpendicular to the BC arm of. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then-
View SolutionCan a quadrilateral ABCD be a parallelogram, if
AB = DC = 8 cm, AD = 4 cm and BC =4.4 cm?
View Solution