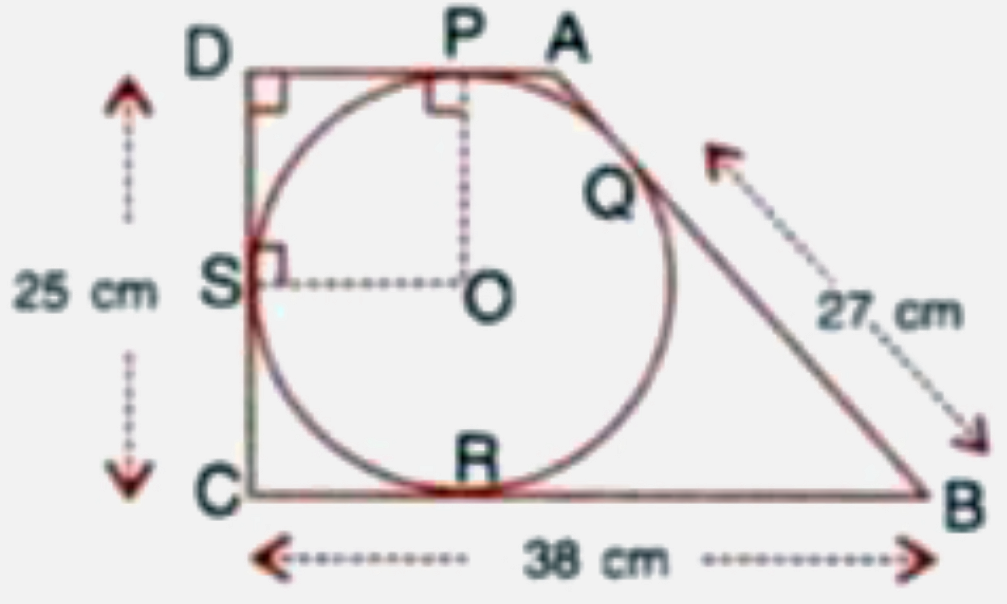
In quadrilateral ABCD angled D=90∘, BC=38cm and DC=25cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27cm. Find the radius of the circle.
28cm
14cm
35cm
19cm
The correct Answer is:B
To find the radius of the inscribed circle in quadrilateral ABCD where angle D is 90 degrees, BC = 38 cm, DC = 25 cm, and QB = 27 cm, we can follow these steps:
Step 1: Identify the lengths of the tangents from points B and C.
- Since QB = 27 cm, and the tangents from a point to a circle are equal, we have:
- BR=BQ=27cm
Step 2: Calculate the length of CR.
- Given that BC = 38 cm, we can find CR:
- CR=BC−BQ=38cm−27cm=11cm
Step 3: Identify the lengths of the tangents from point C.
- Since CR = 11 cm, and the tangents from point C to the circle are equal:
- CS=CR=11cm
Step 4: Calculate the length of DS.
- We know that DC = 25 cm, so we can find DS:
- DS=DC−CS=25cm−11cm=14cm
Step 5: Identify the lengths of the tangents from point D.
- Since DS = 14 cm, and the tangents from point D to the circle are equal:
- DP=DS=14cm
Step 6: Conclusion about the radius.
- The radius of the inscribed circle (r) is equal to the lengths of the tangents from any of the points where the circle touches the sides of the quadrilateral. Therefore, the radius of the circle is:
- r=DS=14cm
Final Answer:
The radius of the inscribed circle is 14 cm.
---
- Since QB = 27 cm, and the tangents from a point to a circle are equal, we have:
- BR=BQ=27cm
Step 2: Calculate the length of CR.
- Given that BC = 38 cm, we can find CR:
- CR=BC−BQ=38cm−27cm=11cm
- Since CR = 11 cm, and the tangents from point C to the circle are equal:
- CS=CR=11cm
- We know that DC = 25 cm, so we can find DS:
- DS=DC−CS=25cm−11cm=14cm
- Since DS = 14 cm, and the tangents from point D to the circle are equal:
- DP=DS=14cm
- The radius of the inscribed circle (r) is equal to the lengths of the tangents from any of the points where the circle touches the sides of the quadrilateral. Therefore, the radius of the circle is:
- r=DS=14cm
The radius of the inscribed circle is 14 cm.
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (B)
Explore 18 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)Book:ICSEChapter:SPECIMEN QUESTION PAPER (MATHEMATICS)Exercise:Section C
Explore 12 Videos
- TRIGONOMETRICAL IDENTITIESBook:ICSEChapter:TRIGONOMETRICAL IDENTITIESExercise:QUESTIONS
Explore 22 Videos
Similar Questions
An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionA circle of radius 4 cm is inscribed in ΔABC, which touches side BC at D. If BD = 6 cm, DC = 8 cm then
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
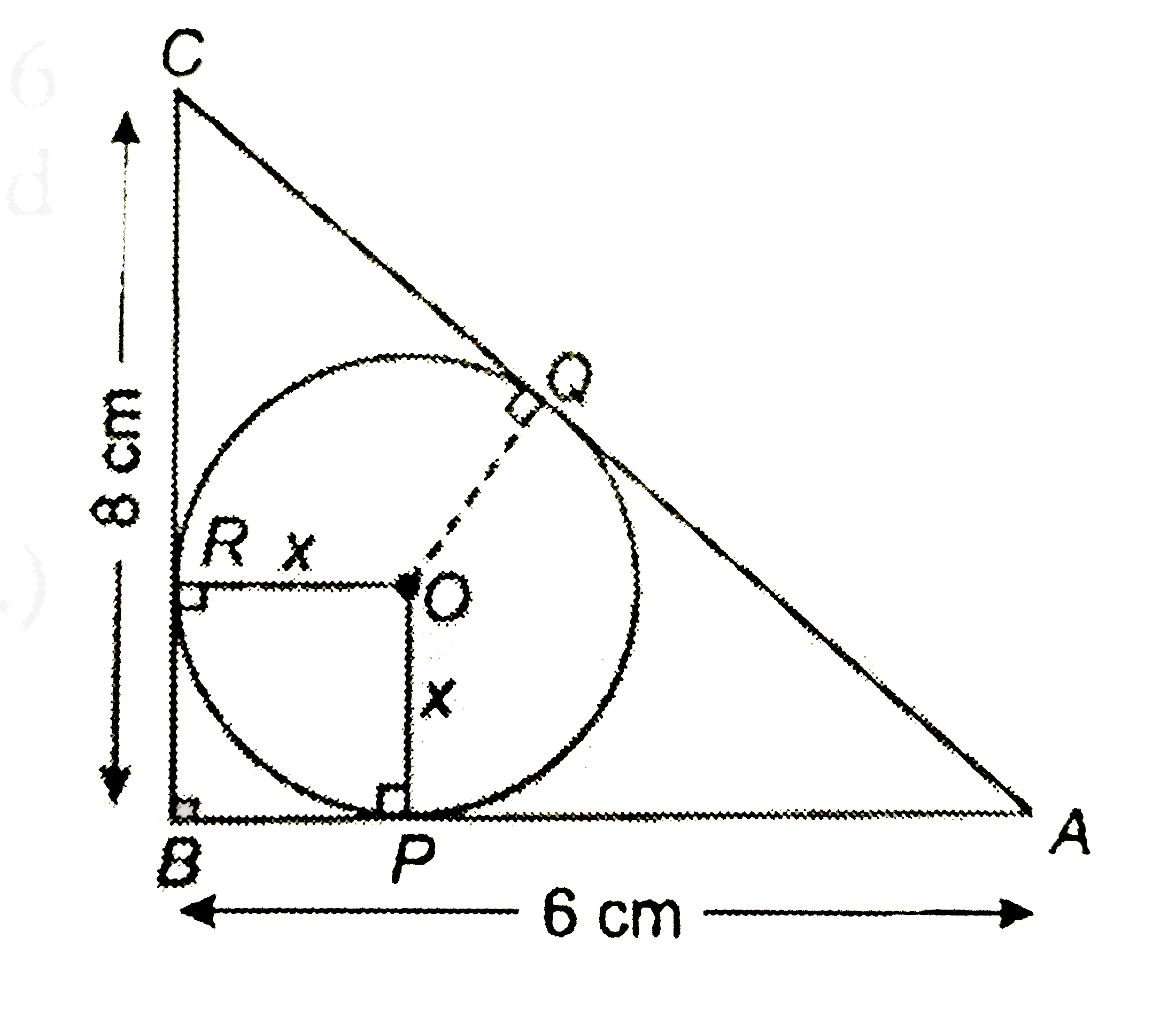
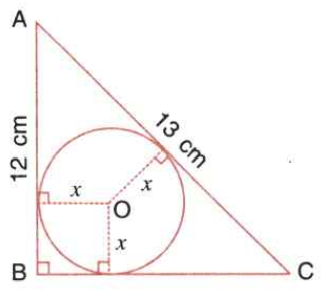
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
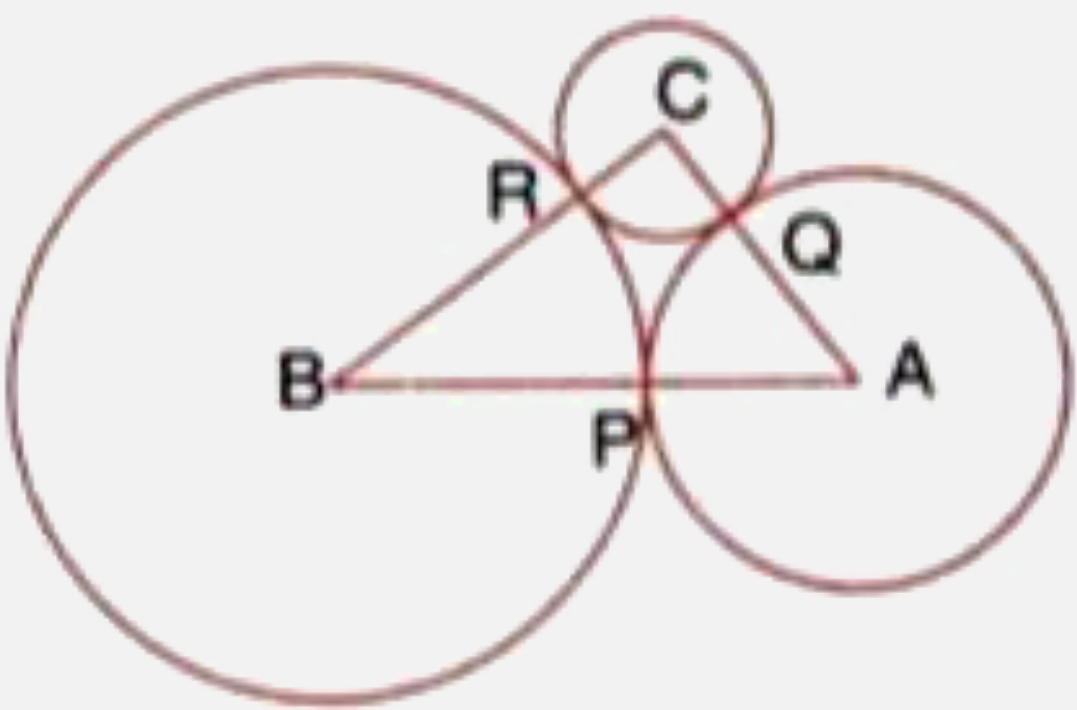
View SolutionABC is a triangle with AB=10cm, BC=8cm and AC=6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres Find the radii of the three circles.
View SolutionIn the following figure, a circle is inscribed in th equadrilaterial ABCD.
 width="80%">
width="80%">
If BC=38 cm, QB=27cm, DC=25 cm and that AD is perpendicular to DC, find the radius of the circle.
View SolutionIn the given figure quadrilateral ABCD is circumscribed and AD⊥DC. Find x if radius of circle is 10 cm.

View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View SolutionABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their cintres. Find the radius of the three circles.

View Solution

