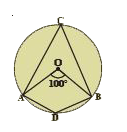
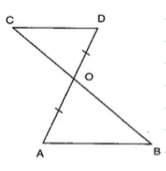
In the given figure PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that:i ∠BAP = ∠ADQii ∠AOB = 2∠ADQiii ∠ADQ = ∠ADB
ii Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
Related Solutions
In the given figure PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment show that
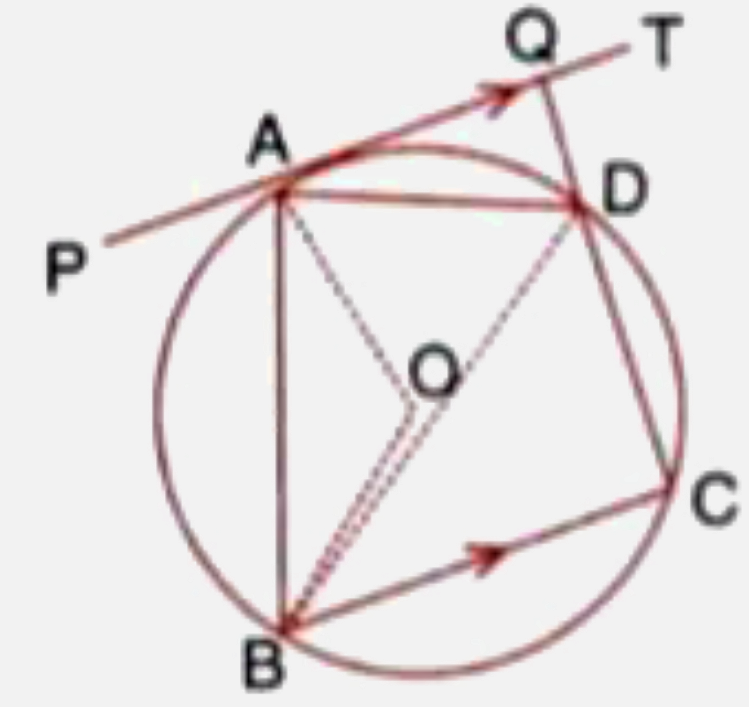
(i)
(ii)
(iii)
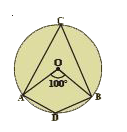
View SolutionIn the figure 'O' is the centre of the circle
find
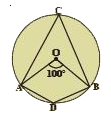
View SolutionIn the figure 'O' is the centre of the circle
find
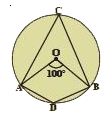
View SolutionIn the figure 'O' is the centre of the circle
find
View SolutionIn the figure 'O' is the centre of the circle
find
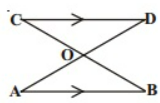
View SolutionIn Figure, line segments is parallel to another line segment is the mid-point of Show that:
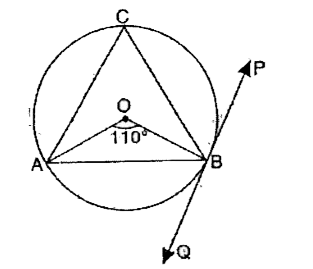
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If , then ABQ is
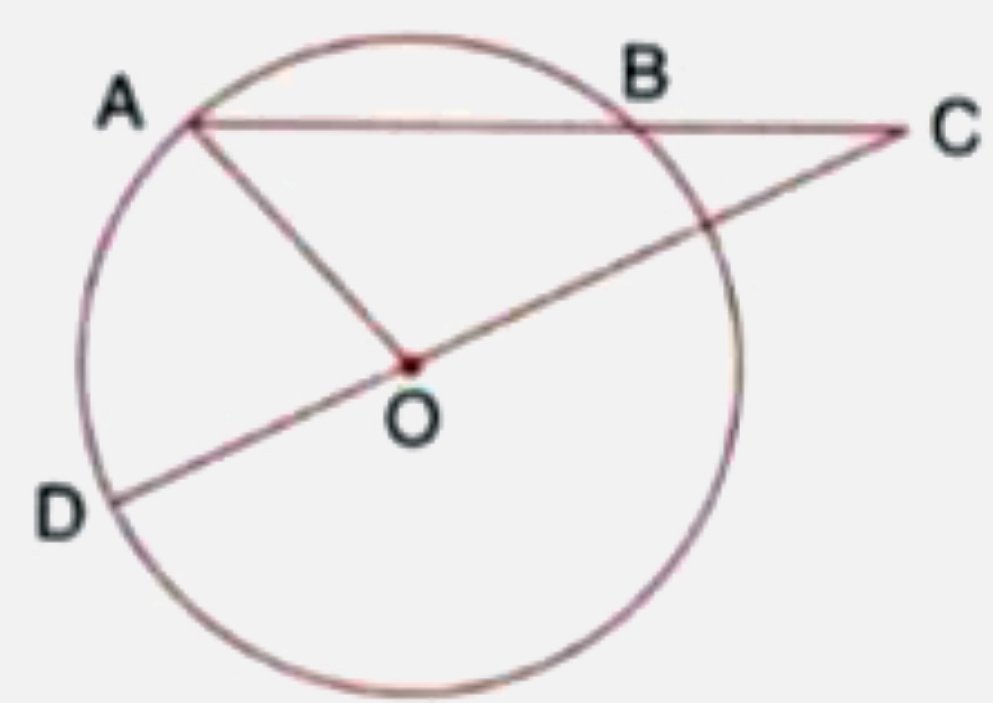
View SolutionIn the figure AB is the chord of a circle with centre O and DOC is a line segment such that . If , find angle AOD.
View SolutionIn Figure, line segment is parallel to another line segment . is the mid-point of . Show that: (i) (ii) is also the mid-point of
View SolutionThe figure shows two circles which intersects at A and B . The centre of the smaller circle is O and lies on the circumference of the Calculate. In terms of , the value of
(i) abtuse
(ii)
Give reassons for your answers clearly.

View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that (i) (ii) O is also the mid-point of BC.
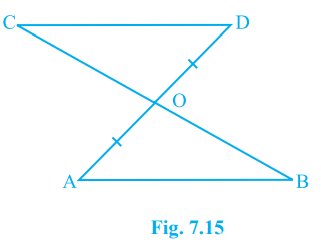
View SolutionIn Figure, line segment is parallel to another line segment . is the mid-point of . Show that: (i) (ii) is also the mid-point of
View SolutionPoint O is the centre of a circle . Line a and line b are
parallel tangents to the circle at P and Q. Prove that
segment PQ is a diameter of the circle.

View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionAB and CD are two parallel tangents to a circle with centre O. ST is a tangent segment between the parallel tangents touching the circle at Q. Show that
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD chord AC.
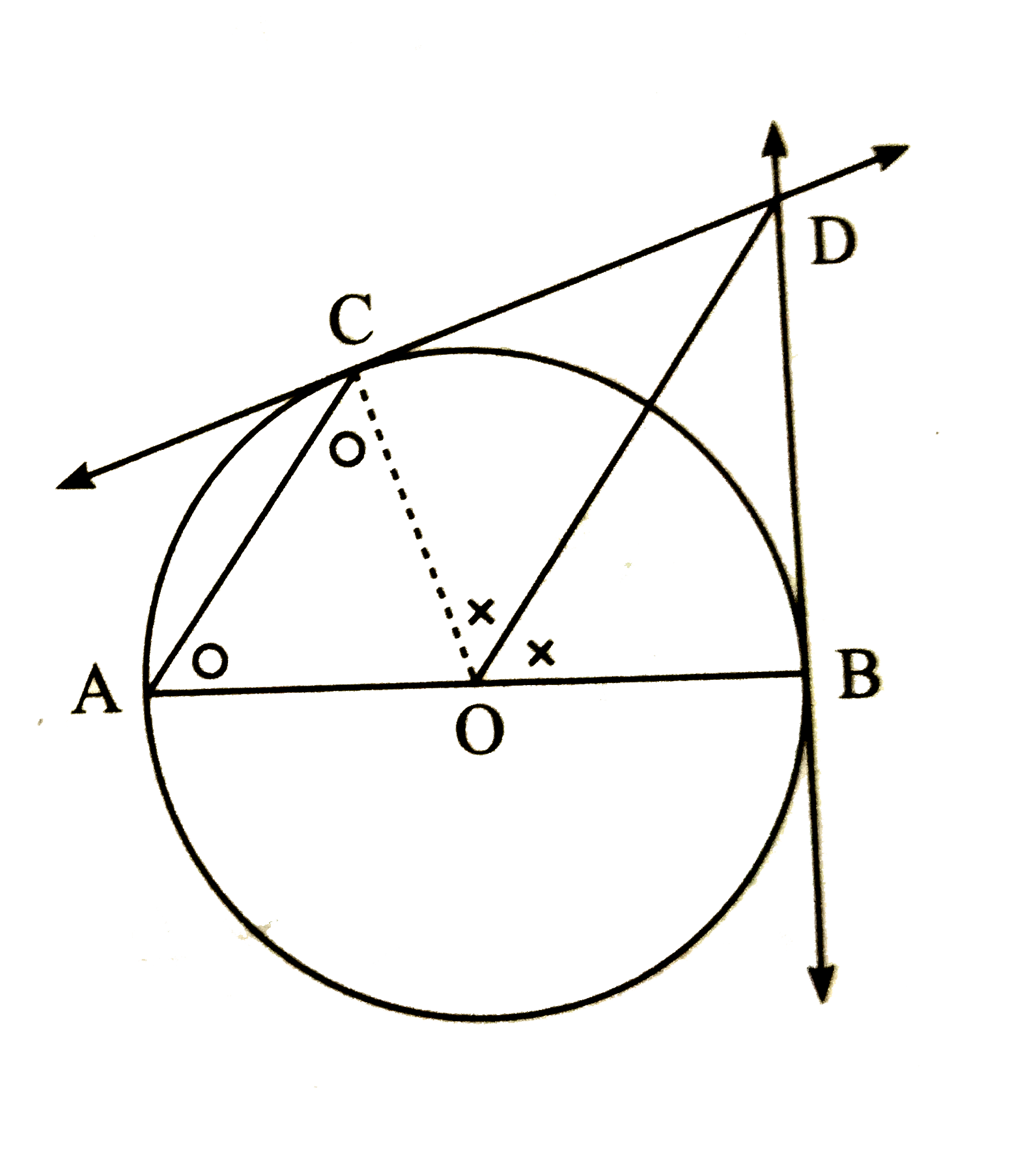
View SolutionLine segment joining any two points on circumference of circle is called chord.
View Solution