An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratio 1:2:3 then find the ratio of the areas of three regions.
Solution:Let the diameters of concentric circles be k 2k and 3k.
Related Solutions
find of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. then find the ratio of the areas of three regions Fig.15.8
View Solutionfind of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio 1:2:3. then find the ratio of the areas of three regions Fig.15.8
View Solutionfind of the An archery target has three regions formed by three concentric circles as shown in Fig 15.8. If the diameters of the concentric circles are in the ratio . , then find the ratio of the areas of three regions Fig. 15.8
View Solutionकिसी धनुर्विद्या (या तीरंदाजी) लक्ष्य के तीन क्षेत्र हैं, जो तीन संकेंद्रीय वृत्तों से बने हैं। यदि इन संकेंद्रीय वृत्तों के व्यास 1:2:3 के अनुपात में हैं, तो इन तीनों क्षेत्रों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
View SolutionAn archery target has three regions formed by three concentric circles as shown in the given figure. If the diameters of the circle are in ratio , then find the ratio of the areas of three regions.

View SolutionAn archery target has three regions formed by three concentric circles in Fig. 12.73. If the diameters of the concentric circles are in the ratio 1:3:5. then find the ratio of the areas of three regions.

View SolutionAs shown in Figure 11.19, an archery target consists of three parts formed by three concentric circles. If the ratio of the diameters of the concentric circles is 1: 2: 3, find the ratio of the areas of those three parts.
View SolutionIf the diameters of the concentric circles shown in the figure below are in the ratio then find the ratio of the areas of three regions.

View SolutionThe diameters of the three concentric circles are in the ratio 1: 2: 3. Find the ratio of their corresponding fields.
View SolutionThe radii of three concentric circles are in the ratio 1:2:3. Find the ratio of the area between the two inner circles to that between the two outer circles.
View SolutionA target shown in Figure, consists of three concentric circles of radii 3,7 and 9cm respectively. A dart is thrown and lands on the target. What is probability that the dart will and on the shaded region?
View SolutionRatio of diameters of three circles are , then ratio of their areas are
View SolutionA target shown in Figure, consists of three concentric circles of radii 3,7 and 9cm respectively. A dart is thrown and lands on the target. What is probability that the dart will and on the shaded region?
View SolutionThe diameters of three circles are in the ratio 3:5:6. If the sum of the circumferences of three circles be 308 cm. Find the difference between the areas of the largest and the smallest of these circles.
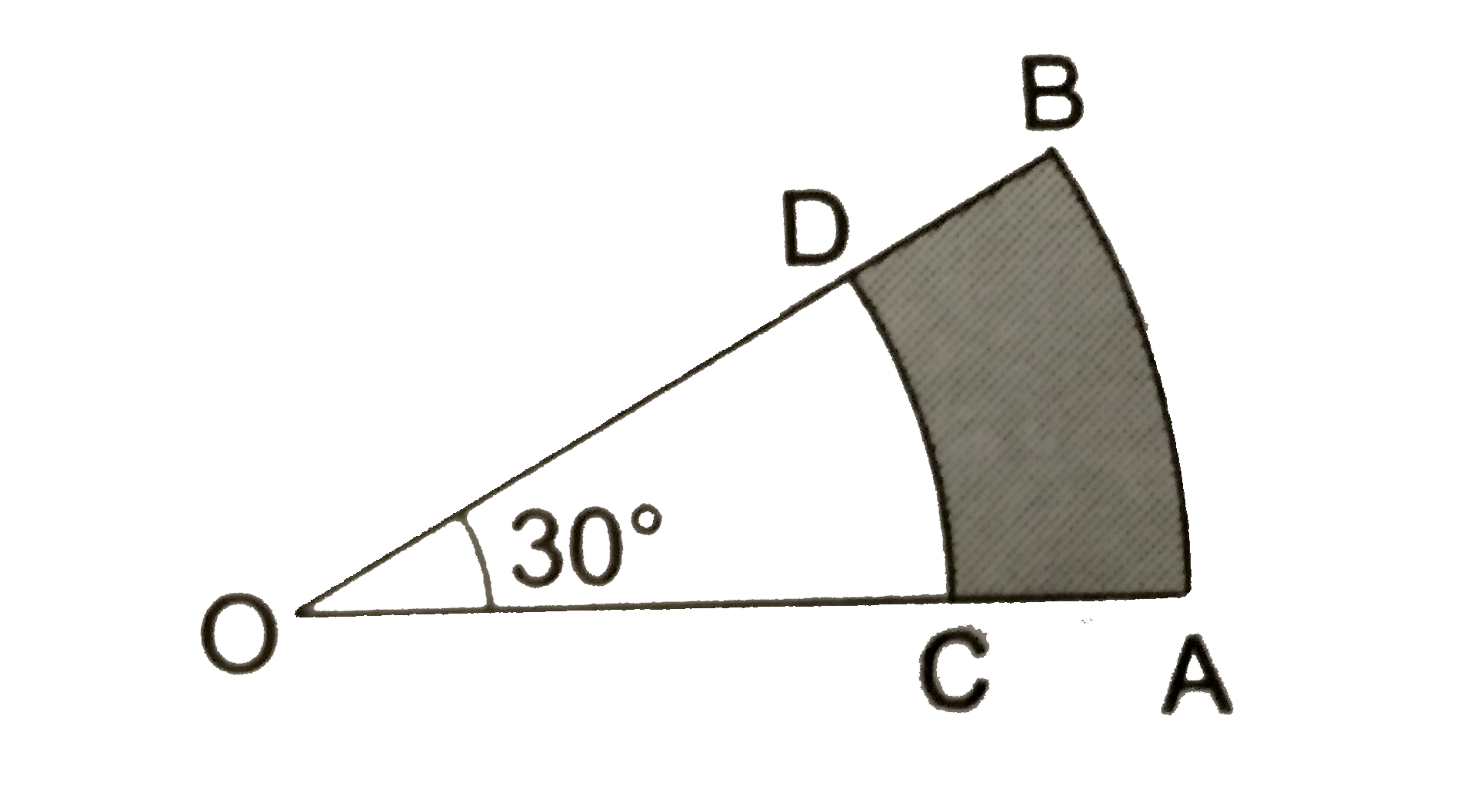
View SolutionTwo concentric circles of radii 3.5 cm and 7cm form a sector as shown in the figure. Find the area of the shaded region.

View SolutionThe radii of three concentric circles are in the ratio 4:57. What is the ratio of the area between the two inner circles to the area between the two outer circles:
View SolutionIf a region bounded by a circle is to be divided into three regions of equal areas by drawing into circles concentric with , then the ratio of the radii of the two circles must be (a) 1 : 3 (b) (c) 1 : 2 (d)
View SolutionPQRS is the diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semi-circles are drawn with PQ and QS as diameters as shown in the figure alongside. Find the ratio of the area of the shaded region to that of the unshaded region.
View SolutionAs shown in the above figure, a circle of radius 3 m is divided into three regions by semicircles of radius 1 m and 2 m. What will be the ratio of the three fields A, B and C?
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
View Solution