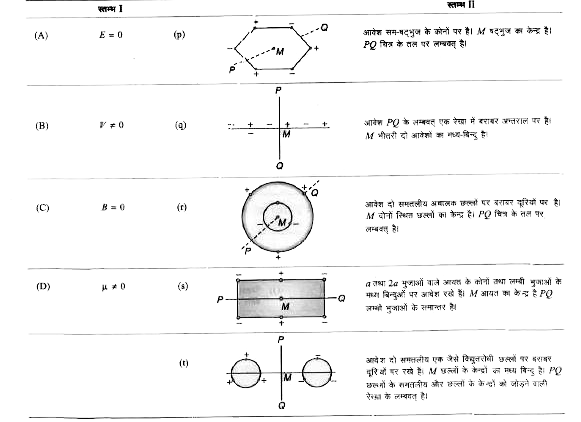
Six point charges each of the same magnitude q are arranged in different manners as shown in Column II. In each case a point M and a line PQ passing through M are shown. Let E be the electric field and V be the electric potential at M potential at infinity is zero due to the given charge distribution when it is at rest. Now the whole system is set into rotation with a constant angular velocity about the line PQ. Let B be the magnetic field at M and μ be the magnetic moment of the system in this condition. Assume each rotating charge to be equivalent to a steady current.Column-I Image Column-II A E=0Charges are at the corners of a regular hexagon. M is the center of the hexagon. PQ is perpendicular to the plane of the hexagon.B V ≠ 0Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the center of the rectangle. PQ is parallel to the longer sides. C B=0Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the center of the rectangle. PQ is parallel to the longer sides.D μ ≠ 0Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the center of the rectangle. PQ is parallel to the longer sides.
B = 0 as current due to rotating charge is zero.μ = 0 as current due to rotating charge is zero.
Related Solutions
Six point charges , each of the same magnitude q, are arranged in different manners as shown in Column II . In each case, a point M and a line PQ passing through M are shown . Let E be the electric field and V be the electric potential at M (potential at infinity is zero ) due to the given charge distribution when it is at rest . Now, the whole system is set into rotation with a constant angular velocity about the line PQ . Let B be the magnetic field at M and be the magnetic moment of the system in this condition . Assume each rotating charge to be equivalent to a steady current .

View SolutionSix point charges, each of the same magnitude q, are arranged in different manners as shown in Column II. In each case, a point M and a line PQ passing through M are shown. Let E be the electric field and V be the electric potential at M (potential at infinity is zero) due to the given charge distribution when it is at rest. Now, the whole system is set into rotation with a constant angular velocity about the line PQ. Let B the magnetic field at M and be the magnetic moment of the system in this condition. Assume each rotating charge to be equivalent to a steady current.
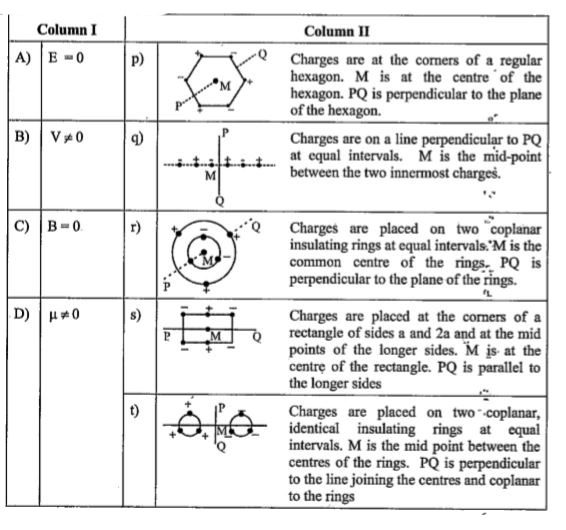
View Solutionस्तम्भ II मे दर्शाए अनुसार 6 बिंदु आवेश, जिसमें से प्रत्येक का परिमाण q है भिन्न भिन्न प्रकार से नियोजित है। प्रत्येक में एक बिंदु M तथा M से जाने वाली एक रेखा PQ दिखाई गई है। मान लें कि जब आवेश स्थिर है तो दिए गए आवेश वितरण के कारण बिंदु M प उत्पन्न विद्युत क्षेत्र E और विद्युत विभव V है (अनन्त पर विभव को शून्य मानें) अब यह आवेश वितरण रेखा PQ के परितः एकसमान कोणीय वेग से घुमाया जाता है । इस स्थिति में बिंदु M पर उत्पन्न चुम्बकीय क्षेत्र B तथा चुम्बकीय आघूर्ण है। प्रत्येक घूमते आवेश को एक स्थिर धारा के बराबर मानें।
View Solutionएक बिंदु आवेश के कारण एक बिंदु पर विद्युत क्षेत्र 20 है और उस बिंदु पर विद्युत विभव 10 है। आवेश से बिंदु की दूरी और आवेश के परिमाण की गणना करें।
View SolutionA charge + Q at A as shown in fig. produces electric field E and electric potential V at D. if we now put charges -2 Q and + Q at B and C respectively , then the electric field and potential at D will be :
View SolutionA charge +Q at A as shown produces electric field E and electric potential V at D. If we now put charges - 3 Q and +Q at B and C, respectively, then the electric field and potential at D will be .
View Solutiona भुजा वाले किसी गहन के प्रत्येक कोने (corner) पर qआवेश स्थित है । ऐसे आवेश वितरण के कारण घन के केंद्र पर विधुत-विभव तथा विधुत-क्षेत्र का परिमाण ज्ञात करें ।
View Solutionएक बिन्दु आवेश से किसी दूरी पर एक बिन्दु A है। A पर वैद्युत क्षेत्र 500 वोल्ट/मीटर तथा विभवांतर 3000 वोल्ट है। बिन्दु आवेश से A की दूरी होगी:
View SolutionFrom a point charge, there is a fixed point A. At a, there is an electric field of 500 V/m and potential difference of 3000 V. Distance between point charge and A will be
View SolutionElectric Potential Basics, Electric Potential due to a point charge, Potential due to cntinuous charge distribution, Ring, Spherical Shell
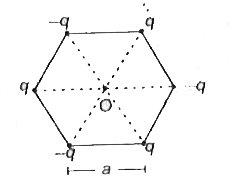
View SolutionSix point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
View SolutionSix point charges are placed at the vertices of a regular hexagon of side a as shown. If E represents electric field and V represents electric potential at O then,
View SolutionThe electrical potential at a certain distance from a point charge is 600V the electric field is 200N//C . The distance of the point charge is….m.
View SolutionThe electric potential and electric field at a point due to a point charge are 600 V and 200 Newton/coulomb respectively, then the magnitude of the point charge is
View SolutionThe points on the line joining two charges +q and 3q (kept at a distance of 1.0 m) where electric potential is zero.
View SolutionElectric field intensity at a point B due to a point charge Q kept at point A is , and electric potential at B due to the same charge is . Calculate the distance and magnitude of charge.
View SolutionTwo point charges +q and -q are separated by a distance d. Except at infinity, where can the electric potential due to these two point charges be zero?
View SolutionThe electric potential at 0.3 m from a point charge is 30 V. What is the magnitude of the charge ?
View SolutionThe electric potential at 0.1 m from a point charge is 90 V. What is the magnitude of the charge?
View Solutionएक ......... उन समस्त बिन्दुओं का समूह होता है जिन पर आवेश वितरण के कारण विद्युत् विभव एक-समान होता है।
View Solution