An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction Fig.14.33. Show that when the ball is pressed down a little and released it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.33].
Volume of the air chamber = VArea of cross-section of the neck = aMass of the ball = mThe pressure inside the chamber is equal to the atmospheric pressure. Let the ball be depressed by x units. As a result of this depression there would be a decrease in the volume and an increase in the pressure inside the chamberDecrease in the volume of the air chamber ΔV = axVolumetric strain = Change in volume/ Original volume⇒ ΔV/V = ax/VBulk Modulus of air B = Stress/Strain = -p/ax/VIn this case stress is the increase in pressure. The negative sign indicates that pressure increases with a decrease in volume.
Related Solutions
An air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal.
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
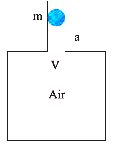
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
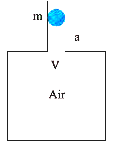
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass mjust fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27
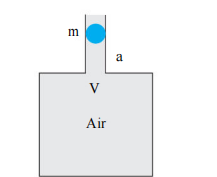
View SolutionAn air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
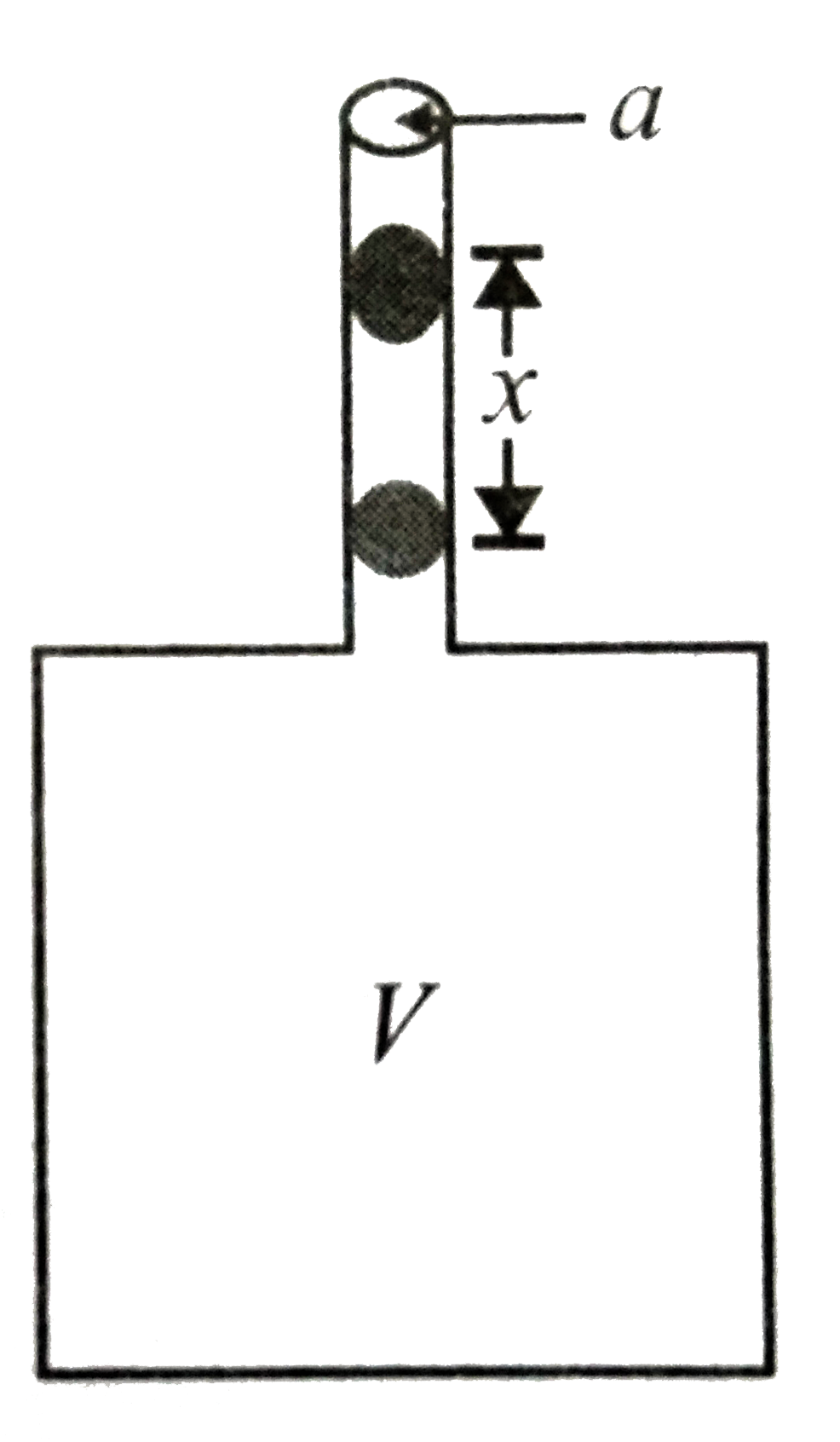
View SolutionAn air champer of volume 'V' has a neck area of cross - section A into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillation assuming pressure volume variations of air to to be isothermal.
View SolutionAn air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time periodof oscillations assuming pressure volume variatinos of air to be isothermal.
View SolutionAn air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction. When the ball is pressed down a little and released, it executes SHM. The time period is assuming pressure, volume variations of air to be isothermal, B = bulk modulus)
View SolutionAn air chamber of volume V has a neck of cross-sectional area 'a' into which a light ball of mass (m) can move without friction. The diameter of the ball is equal to that of neck of chamber. The ball is pressed down a little and relaxed. If bulk modulus of air is B, the time period of resulting oscillation of ball is given by:
View SolutionAn air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. Consider diameter of the ball to be equal to that of the neck of the chamber. The ball is then pressed down a little and released. Let the bulk modulus of air is B. The time period of the oscillation of the ball is:
View SolutionAn air chamber of volume V has a neck of crosssectional area "a' into which a light ball of mass "m' just fits and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released. If the bulk modulus of air is B the time period of the oscillation of the ball is 2pi m ^(x) V ^(y) B ^(z) a ^(9). The value of (xy)/(q) is
View SolutionAn air chamber of volume has a long of cross sectional area . A ball of mass is fixed sympthlly in the track The ball modulus of air is ball is pressed down slightly and released, the time period of the oscillation is
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
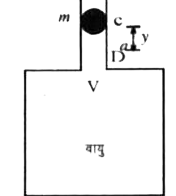
View Solutionचित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल A है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं, तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए।
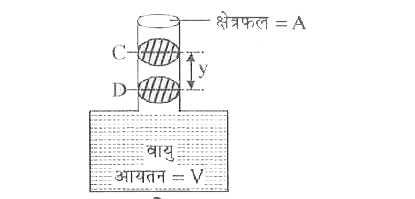
View Solutionचित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन ) की अनुप्रस्थ काट का क्षेत्रफल a है इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है | यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते है, तो वह सरल आवर्त गति करती है दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए [चित्र देखिए ] |
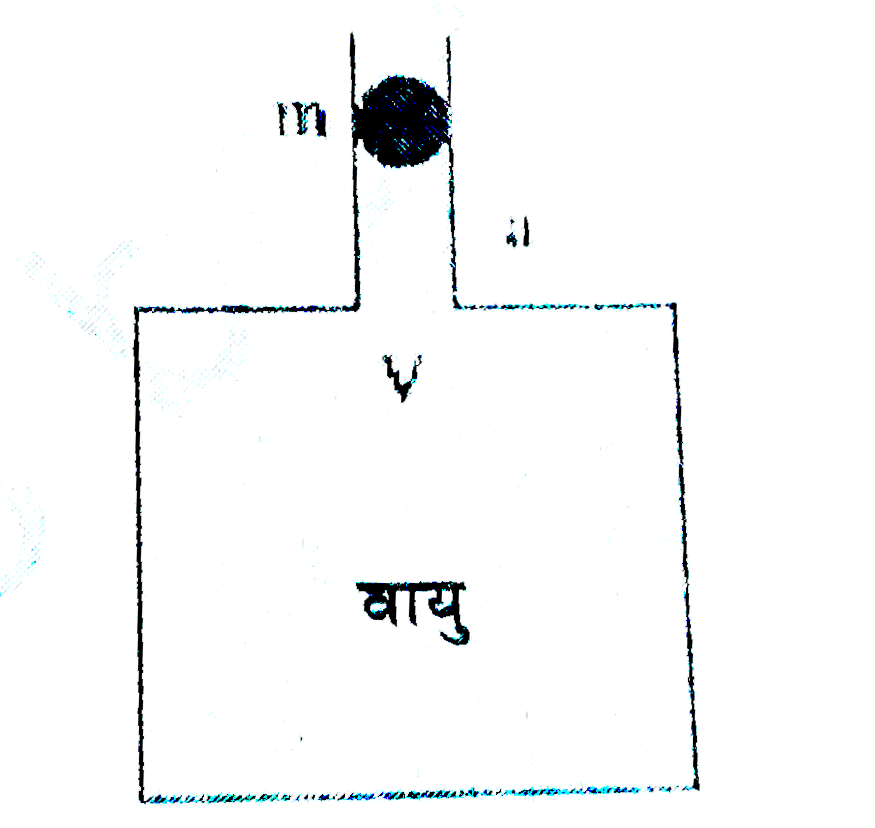
View Solutionचित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल a है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना घर्षकेँ के ऊपर निचे गति कर सकती है। यह दर्शाइए की जब गोली को थोड़ा निचे दबा कर मुक्त छोड़ देते है। तो वह सरल आवर्त गति करती है। दाब आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए
View SolutionA ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V_(0) when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P_(0) . If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
View SolutionA cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (figure). If the temperature is increased

View SolutionA cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Fig.) If the temperature is increased,

View Solution