D is the mid-point of side BC of ∆ABC and E is the mid-point of BD. if O is the mid-point of AE prove that ar ∆BOE = 1/8 ar ∆ ABC.
Given that D is the midpoint of side BC of ∆ABC. E is the midpoint of BD and O is the midpoint of AE Since AD and AE are the medians of ∆ABC and ∆ABD respectively
Related Solutions
D is the mid-point of side BC of Delta ABC and E is the mid-point of BO. If O is the mid-point of AE, then ar( Delta BOE) = 1/k ar( Delta ABC). Then k equals
View Solutionमें भुजा BC का मध्य-बिंदु D है तथा BD का मध्य-बिंदु E है। यदि AE का मध्य-बिंदु O हो तो, सिद्ध कीजिए कि
View SolutionDelta ABC In BC, if D is the mid-point of the side BC and E is the mid-point of the median AD, then ar( Delta BED) = ?
View SolutionD is the mid-point of BC of . E and O are the mid-points of BD and AE respectively. Then the area of the triangle BOE is-
View SolutionIf D, E, f are the mid-point of the sides of triangle ABC, prove that : .
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that: ar(triangleBED) = 1/4 ar(triangleABC)
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of
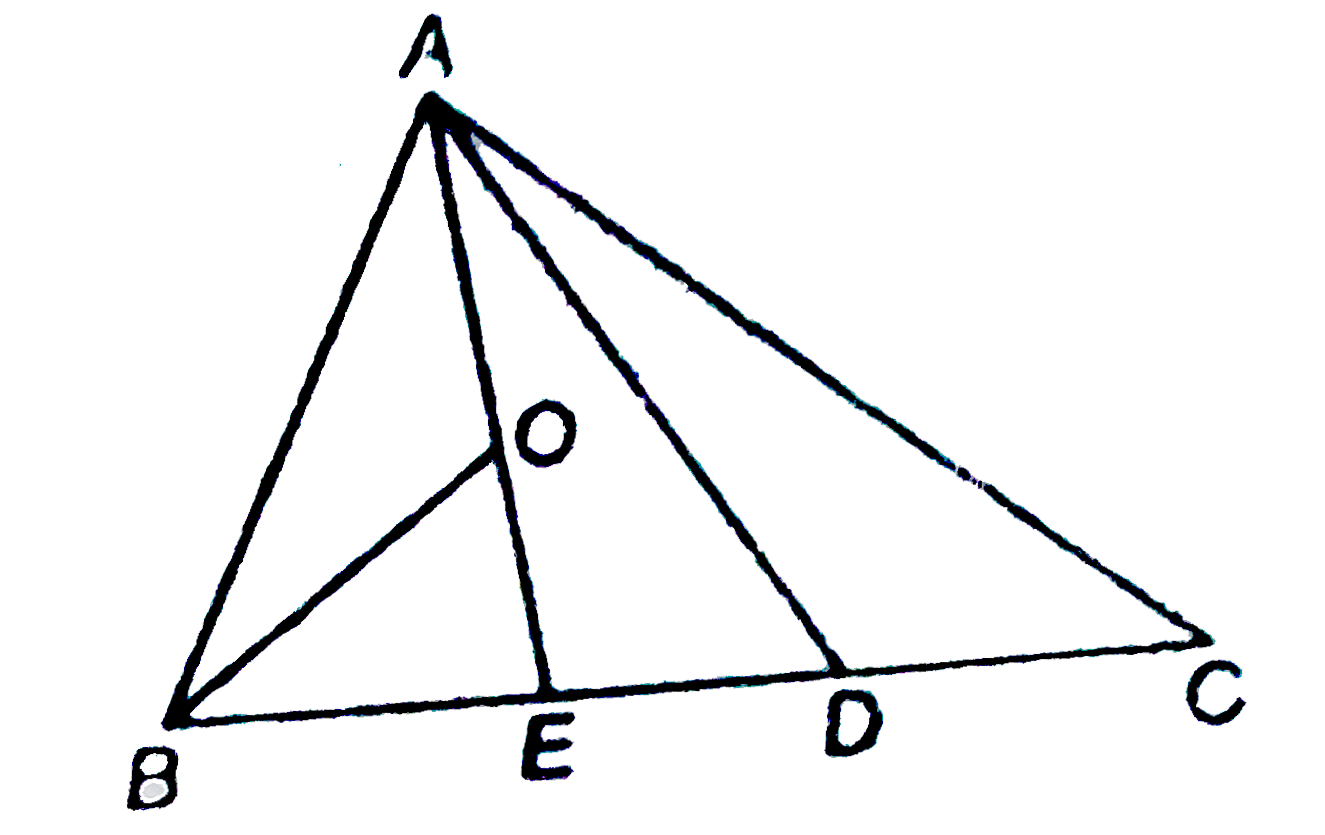
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of

View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BDE) = 1/4 ar(ABC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(FED) = 1/8 ar(AFC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)= ar(ABC).
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BDE) = 1/2 ar(BAE)
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (
View SolutionIn triangleABC,D is the mid-point of AB and P is point on BC. If CQ||PD meets AB in Q then prove that : ar(BPQ) = 1/2 ar(ABC)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of the triangle ABC respectively. show that ar (Delta DEF) = (1)/(4) ar (DeltaABC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, .
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, .
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BFE) = ar(AFD)
View SolutionP and Q are respectively the midpoints of sides AB and BC or a triangle ABC and R is the mid-point of AP, show ar(RQC) = ar(ABC).
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid point at AP, show that
(i) ar (PQR) = ar (ARC)
(ii) ar (RQC) = ar (ABC)
(iii) ar (PBQ) = ar (ARC)
View Solution