In the above question point C is called a mid-point of line segment AB prove that every line segment has one and only one mid-point.
Let there be two mid-points C and D.C is the mid-point of AB. AC = CBAC + AC = BC + AC Equals are added on both sides … 1Here BC + AC coincides with AB. It is known that things which coincide with one another are equal to one another.∴ BC + AC = AB … 2It is also known that things which are equal to the same thing are equal to one another. Therefore from equations 1 and 2 we obtain AC + AC = AB⇒ 2AC = AB … 3Similarly by taking D as the mid-point of AB it can be proved that 2AD = AB … 4From equation 3 and 4 we obtain2AC = 2AD Things which are equal to the same thing are equal to one another.⇒ AC = AD Things which are double of the same things are equal to one another. This is possible only when point C and D are representing a single point.Hence our assumption is wrong and there can be only one mid-point of a given line segment.
Related Solutions
In question I, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.

View SolutionIn question 4, point C is called a mid-point of line segment AB. Prove that every line segment has only one mid-point.
View SolutionIn Question 4, point 'C' is called a midpoint of line segment AB. Prove that every line segment has one and only one mid point.
View SolutionIn question 4, C is called a mid-point of the line segment AB. Prove that a line segment has one and only one mid-point.
View SolutionIn Question 4,
().
Point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
View SolutionProve that every line segment has one and only one mid-point.
View Solutionप्रश्न 4 में, C रेखाखंड AB एक मध्य-बिंदु कहलाता है | सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है |
View SolutionIn Q.4, point C is called a midpont of line segment AB. Prove that every line segment has one and only one midpoint.
View SolutionA point C lies between two points A and B such that AC = BC, then . Point C is called a midpoint of line segment AB. Prove that every line segment has one and only one midpoint.
View Solutionप्रश्न 4 में, C रेखाखंड AB एक मध्य-बिंदु कहलाता है | सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है |
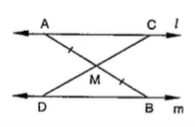
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.
View SolutionMid point of a line Segment
View SolutionShow that every line segment has one and only one middle point.
View Solutionदो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित हैं कि AC = BC तो , C रेखाखंड AB का एक मध्य - बिंदु कहलाता हैं । सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य - बिंदु होता हैं ।
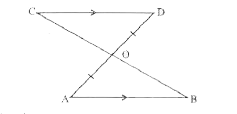
View Solutionरेखाखण्ड AB एक अन्य रेखाखण्ड CD के समान्तर है और O रेखाखण्ड AD का मध्य-बिन्दु है | दर्शाइए कि
(i) ~-=
(ii) O, रेखाखण्ड BC का मध्य बिन्दु है |
View SolutionFind the mid points of the line segment joining the points .
View SolutionIn Figure, line segments is parallel to another line segment is the mid-point of Show that: is also the mid-point of
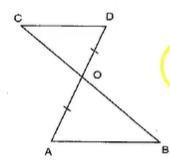
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD. Show that O is also the mid - point of BC .
View SolutionShow that the mid-point of the line segment joining the points and is also the mid-point of the line segment joining the points and .
View SolutionIn Figure, and M is the mid-point of the line segment Prove that is also the mid-point of any line segment having its end-points on and respectively.
View Solution