O is any point in the interior of ΔABC. Prove thati AB + AC > OB + OCii AB + BC + CA > OA + QB + OCiii OA + OB + OC >1/2 x AB + BC + CA
Given that O is any point in the interior of ΔABC.We have to provei AB + AC > OB + OCii AB + BC + CA > OA + QB + OCiii OA + OB + OC >1/2 x AB + BC + CAWe know that in a triangle the sum of any two sides is greater than the third sideSo we haveNow extend or produce BO to meet AC in D.Now in ΔABD we haveSimilarly in ΔODC we haveOD+DC>OC ....5i Adding 4 and 5 we getii Adding equation 6 7 and 8 we getiii Adding equations 1 2 and 3
Related Solutions
is any point in the interior of Prove that
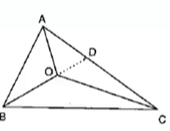
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
View SolutionLet O be any point in the interior of , prove that :
View SolutionLet O be any point in the interior of , prove that :
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
View Solution'O' is any point in the interior of a Delta ABC prove that AB+BC+CA>OA+OB+OC
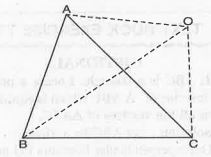
View SolutionO is any point in the exterior of a . Prove that
 .
.
View SolutionO is any point in the exterior of a . Prove that
 .
.
View SolutionA point O lies inside a . Show that .
View SolutionThe point O is outside the . Show that .
View SolutionIf O is point in the exterior of ,show that
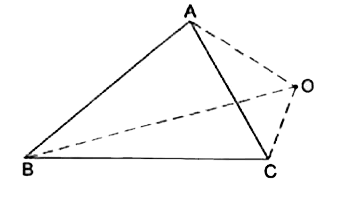
View SolutionIf 0 is a point in the exterior of an ABC, then show that OA+OB +OC gt (1)/2 (AB + BC + CA)
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the be any points, then prove that
View SolutionIf , and are the mid-points of the sides , and respectively of the and be any point, then prove that
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the be any points, then prove that
View SolutionIf , and are the mid-points of the sides , and respectively of the and be any point, then prove that
View SolutionO is a point within the . P, Q , R are three points on OA , OB and OC respectively such that and . Prove that .
View SolutionIf OABC be a regular tetrahedron such that then
View SolutionIf OABC is a tetrahedron such that then
View SolutionThe OABC is a tetrahedron such that ,then
View Solution