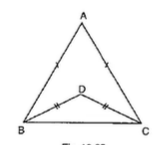
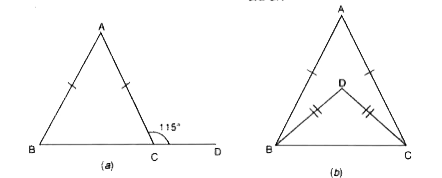
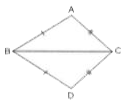
In Fig. 10.25 AB = AC and DB = DC find the ratio ∠ABD : ∠ACD.
Consider the figureGivenAB = AC DB = DC and given to find the ratio∠ABD = ∠ACDNow ΔABC and ΔDBC are isosceles triangles since AB = AC and DB = DC respectively⇒ ∠ABC =∠ACB and ∠DBC = ∠DCB [angles opposite to equal sides are equal]Now consider ∠ABD : ∠ACD
Related Solutions
In Figure, find the ratio
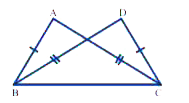
View SolutionIn the fig. AB=AC and DB=DC. Prove that angleABD=angleACD
View SolutionIf AB = AC was DB = DC, then angleABD : angleACD Find
View SolutionAB = Dc and . Prove that:
AC = DB
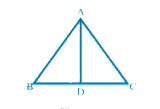
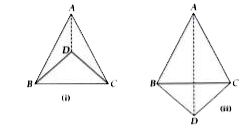
View SolutionABC is an isosceles triangle with AB = AC and D is the mid-point of base BC.
(a) State three pairs of equal parts in the triangles ABD and ACD.
(b) Is . If so why?
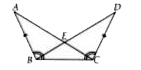
View SolutionIf are on the same base BC, AB = DC and AC = DB, then which of the following gives a congruence relationship?
View SolutionABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of and .
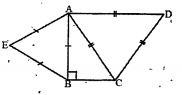
View SolutionIn Fig , ABD is a triangle right angled at A and show that
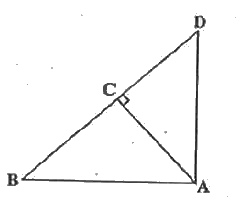
View SolutionIn Figure, Prove that
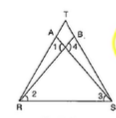
View Solutionआकृति में और सिद्ध करें कि .
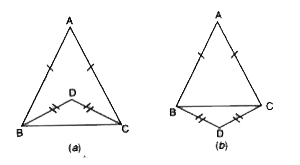
View Solutionआकृति B में, तथा तब
View Solutionचित्र में, AB=AC तथा DB=DC सिद्ध कीजिएः .
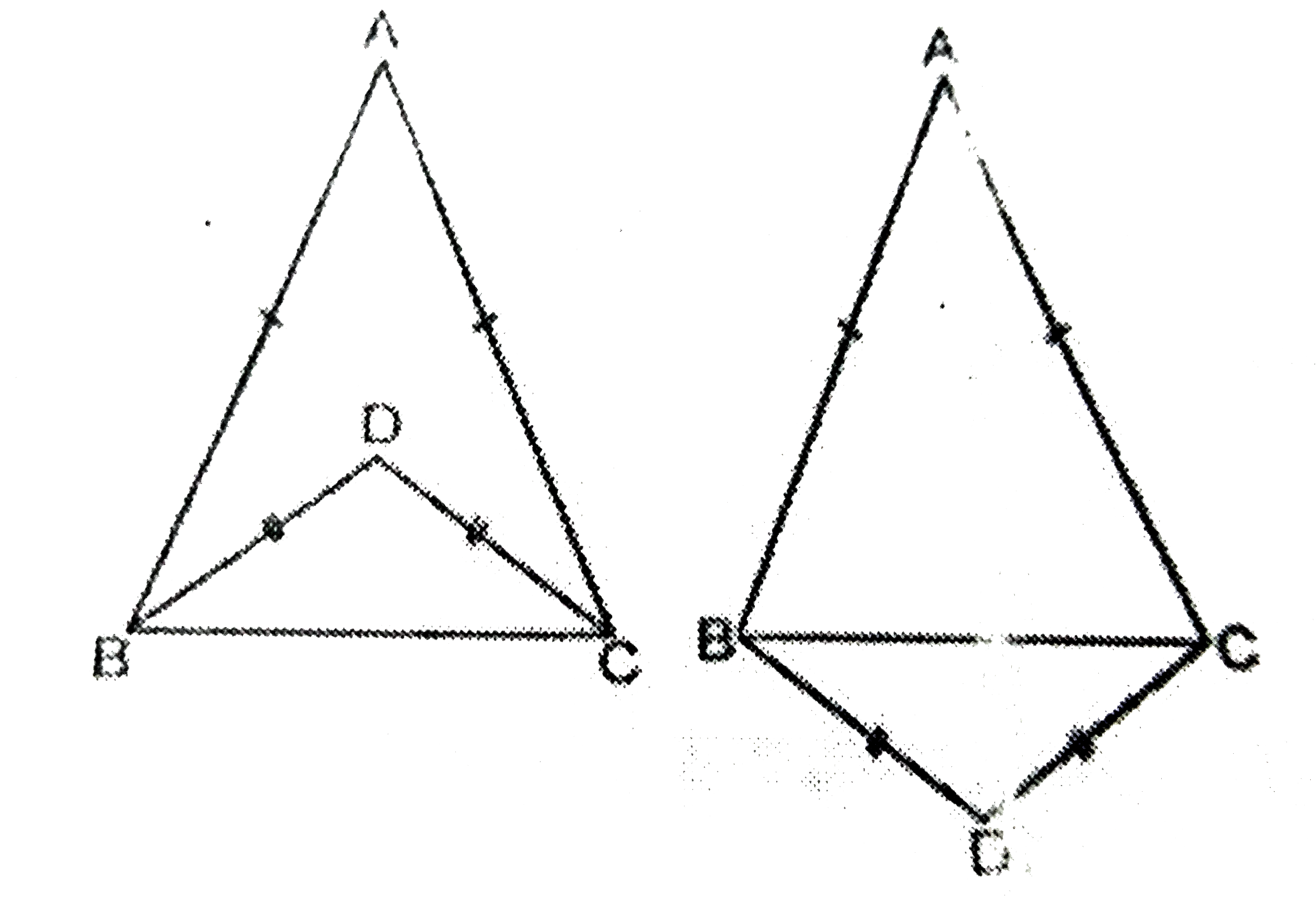
View SolutionIn both the given figures, AB = AC and DB = DC. Prove that .
View SolutionIn the figure given below, AB= DC and AC=DB. Is ?
View SolutionIn the parsed image, AB = AC And /_DAB = /_CAD , So what ∆ACD And ∆ABD Are congruent? If so, why?
View SolutionIn , if is the bisector of , prove that:
View SolutionIn the given figure, AB = DB and AC = DC. If , find the values of x and y.
View SolutionOne DeltaABC The equilateral triangles ABD and ACE on the sides AB and AC are drawn such that the vertices D and E, DeltaABC Prove that BE=DC
View SolutionArea of quadrilateral ACDE is , B is the mid-point of AC. Find the area of if :
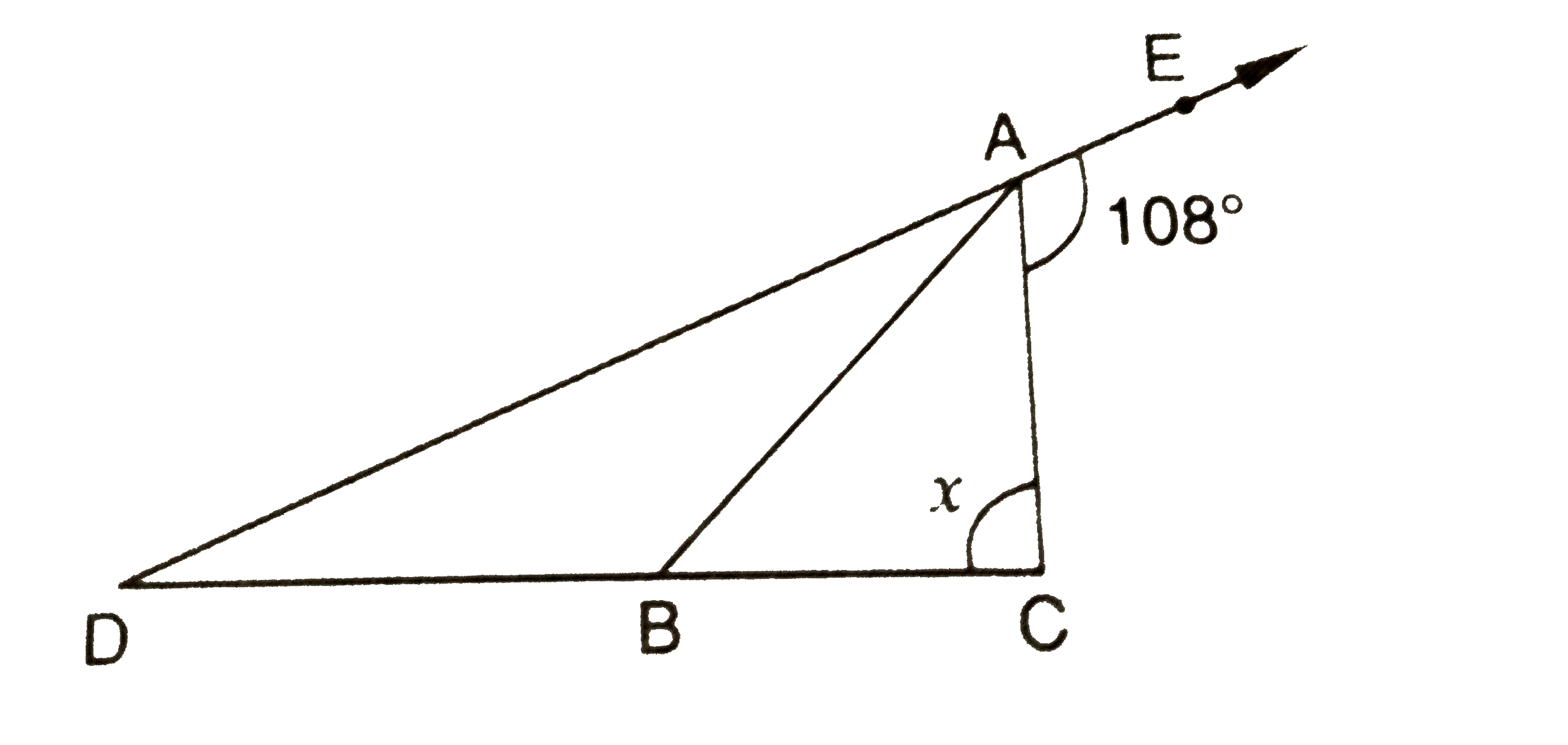
View Solutionचित्र 9.35 में, यदि AB कोण को 1 : 3 के अनुपात में विभाजित करती है तथा AB = DB हो, तो x का मान ज्ञात कीजिए।
View Solution