The potential energy function for a particle executing linear SHM is given by Vx = 1/2kx2 where k is the force constant of the oscillator Fig. 6.2. For k = 0.5N/m the graph of Vx versus x is shown in the figure. A particle of total energy E turns back when it reaches m x = ±xm . If V and K indicate the P.E. and K.E. respectively of the particle at x = +xm then which of the following is correct?a V = O K = Eb V = E K = Oc V < E K = Od V = O K < E.
b V = E K = O
Related Solutions
The potential energy function for a particle executing linear SHM is given by wher e k is the force constant of the oscillator (figure). For k = 0.5 N/m ,the graph ofV(x) versus x is shown in the figure . A particle of total energy E turns back when it reaches . If V and K indicate the PE and KE , respectively of the particle at , then which of the following is correct ?

View SolutionThe potential energy function for a particle executing linear SHM is given by where k is the force constant of the oscillator. For , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches .if V and K indicate the potential energy and kinetic energy respectively of the particle at ,then which of the following is correct?
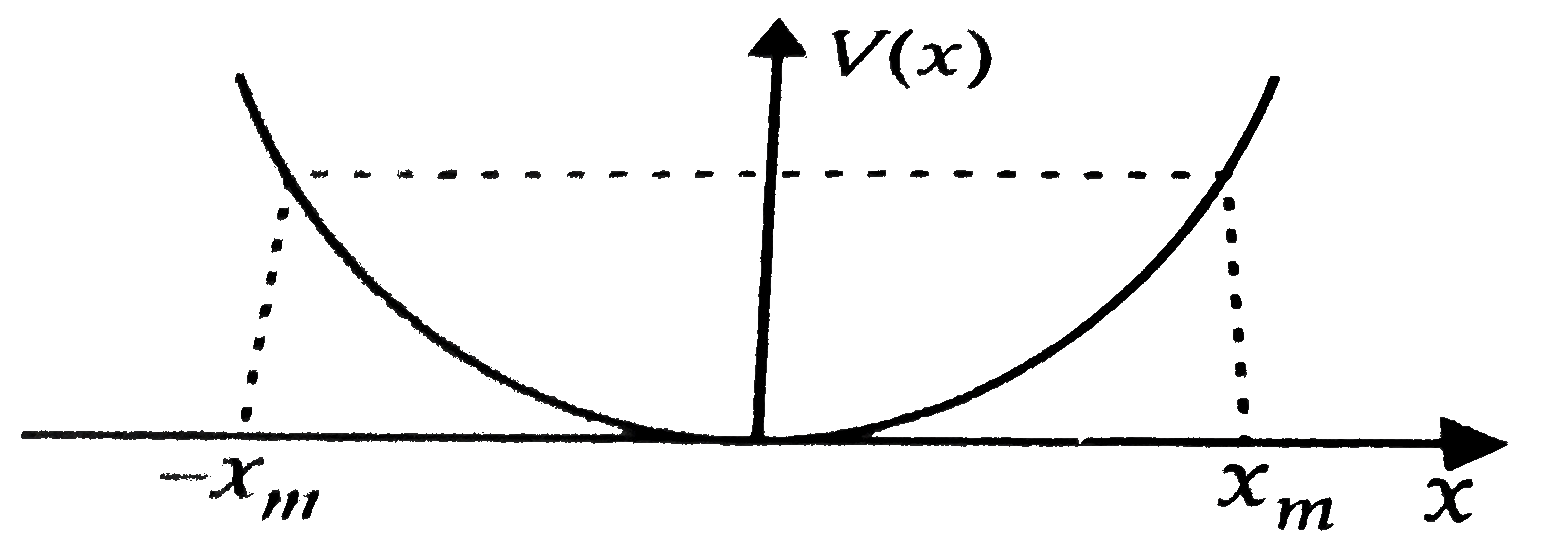
View SolutionThe potential energy function for a particle executing linear SHM is given by where k is the force constant of the oscillator. For , the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches .if V and K indicate the potential energy and kinetic energy respectively of the particle at ,then which of the following is correct?

View SolutionTo potential energy function for a particle executing linear simple harmonic motion is given V(x) = kx^(2) //2 , where k is the force constant of the oscillator . For k = 0.5 N m^(-1) the graph of V(x) versus x is shown in Fig. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x = pm 2 m
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by V(x) =kx^2/2, where k is the force constant of the oscillator. For k = 0.5 N ^-1 , the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.,br>
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by where k is the force constant of the oscillator . For , the graph of V(x) versus x is shown in figure . Show that a particle of total energy 1 J movng under this potential must 'turn back ' when it reaches .

View Solutionसरल आवर्त गति (SHM) करते किसी कण का स्थैितिज ऊर्जा फलन है - जहाँ k दोलित्र का बल नियतांक है। k = 0.5N/m के लिए V(x) और x का ग्राफ चित्र 6.2 में दर्शाया गया है। E ऊर्जा का कोई कण पर पहुँच कर वापस लौटता है। यदि पर V एवं K क्रमशः कण की स्थैितिज ऊर्जा (P.E.) एवं गतिज ऊर्जा (K.E.) निरुपित करते हों तो निम्नलिखित में कौन-सा कथन सही है?
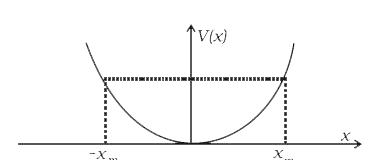
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by V(x)= kx^(2)"/"2 , where k is the force constant of the oscillator. For k= 0.5 Nm^(1) , the graph of V(x) versus x is shown in Fig. 6. 12. Show that a particle of total energy 1 J moving under this potential must 'turn back' when it reaches x= pm 2m .
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given by V{x) = kx^2//2 , wherek is the force constant of the oscillator. For k = 0.5 N m^-1 , the graph of V[x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x =overset+- 2 m.
View Solutionसरल रेखीय गति कर रहे किसी कण के लिए स्थितिज ऊर्जा फलन को के द्वारा निरूपित किया जाता है, जहाँ दोलित्र का बल गुणांक है। के लिए, V(x) बनाम x के आरेख को चित्र में दर्शाया गया है। कुल ऊर्जा E का कण उस समय वापस हो जाता है जब यह पर पहुँचता है। यदि पर किसी कण की स्थितिज व गतिज ऊर्जा को क्रमश: V व K के द्वारा दर्शाया जाता है, तब निम्न में से कौन-सा सही है?
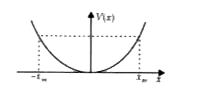
View SolutionThe potential energy function for a particle executing linear simple harmonic motion is given U(x)=1/2kx^(2) , where k is the force constant of the oscillator. For k=0.5 Nm^(-1) , the graph of U(x) on Y-axis x is shown figure. The particle has total energy 1J. Moving this potential it turns back when it reaches x=+- _________m
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x) = k|x|^3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle of mass m is executing oscillations about the origin on X-axis. Its potential energy is, where K is a positive constant. If the amplitude of oscillation is a, then its time period T is:
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|^(2) , where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
View Solution