A4 2 B6 5 and C1 4 are the vertices of ΔABC.i The median from A meets BC in D. Find the coordinates of the point D.ii Find the coordinates of point P on AD such that AP : PD = 2 : 1.iii Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : l and CR : RF= 2 : 1.iv What do you observe?
i Median AD of the triangle will divide the side BC in two equals parts. So D is themidpoint of side B.Coordinates of Dii Point P divides the side AD in a ratio 2:1Coordinates of Piii Median BE of the triangle will divide the side AC in two equal parts. So E is the midpoint of side AC.Point Q divides the side BE in a ratio 2:1Median CF of the triangle will divide the side AB in two equal parts. So F is the midpoint of side AB.iv Now we may observe that coordinates of point P Q R are same. So all these are representing same point on the plane i.e. centroid of the triangle.
Related Solutions
The points A are the vertices of ABC.
(i) The median from A Meets Bc at D. Find the coordinates of the points D.
(ii) Find the coordinates of the point P on Ad such that .
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that .
What are the coordinates of the centroid of the ABC?
View SolutionThe points A are the vertices of ABC.
(i) The median from A Meets Bc at D. Find the coordinates of the points D.
(ii) Find the coordinates of the point P on Ad such that .
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that .
What are the coordinates of the centroid of the ABC?
View SolutionLet A (4, 2), B(6, 5) and C(1, 4) be the vertices of .
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
View Solution7. Let A (4, 2) B(6.,5) and C(1.,4). be the vertices of DeltaABC. (1) The median from A meets BC at D. Find the coordinates of the point D. (2) the coordinates of the point P on AD such that AP: PD= 2:1. (3) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ: QE = 2 :1 and CR :RF =2: 1. (4) what do yo observe?
View Solutionऔर एक के शीर्ष हैं।
(i) A से खींची गई माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित उस बिंदु P के निर्देशांक ज्ञात कीजिए, जिससे AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर स्थित क्रमश: ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2:1 और CR : RF = 2:1 हो।
(iv) के केंद्रक के क्या निर्देशांक हैं?
View SolutionLet A(4,2) , B(6,5) and C(1,4) be the vertices of the . The median from A meets BC at D. Find the coordinates of the point D. Find the coordinates of the point P on AD such that AP : PD = 2 : 1 .
View SolutionLet A (4, 2), B(6, 5) and C(1, 4) be the vertices of .
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
(v) If and are the vertices of ∆ ABC, find the coordinates of the centroid of the triangle.
View SolutionLet a(4, 2), B(6, 5) and C(1, 4) be the vertices of .
Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
View SolutionLet (4, 2), B (6, 5) and C (1, 4) be the vertices of . :- Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
View Solutionमाना ले कि के शीर्ष और है
(i ) A से खींची गई मध्यिका आधार BC से D पर मिलती है |D का निर्देंशाक ज्ञात कीजिए |
(ii) AD पर स्थित बिंदु P का निर्देशक ज्ञात करे यदि P ,AD पर इस तरह स्थित है की AP : PD 2: 1
(iii) मध्यिकाए BE और CF पर स्थित बिन्दुऔ Q और R के निर्देशाक ज्ञात करे जिससे BQ : QE = 2: 1 और CR : RF =2 : 1
(iv) आप क्या निरिक्षण करते है |
View Solutionयदि और एक त्रिभुज ABC के शीर्ष हैं । यदि शीर्ष A से खींची गई माध्यिका भुजा BC को पर D काटती है, तो
(i) बिन्दु D के निर्देशांक ज्ञात कीजिए ।
(ii) माध्यिका AD पर एक बिन्दु P इस प्रकार हो कि , तो P के निर्देशांक ज्ञात कीजिए ।
(iii) माध्यिकाओं BE और CF पर क्रमशः Q और R बिन्दुओं के निर्देशांक ज्ञात कीजिए जबकि और है ।
तुम क्या प्रेक्षण (observe) करते हो ?
View SolutionAD is the median on BC. Find the coordinates of the point D
View SolutionAD is the median on BC. Find the coordinates of the point D
View SolutionAD is the median on BC. Find the coordinates of the point D
View SolutionLet (4, 2), B (6, 5) and C (1, 4) be the vertices of . :- Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
View SolutionFind the coordinates of points Q and R on medians BE and CF respectively such that BQ:CF =2:1 and CR:RF =2:1
View SolutionFind the coordinates of the point P on AD such that AP : PD = 2 : 1.
View SolutionFind the coordinates of the point P on AD such that AP : PD = 2 : 1.
View SolutionLet A(4,2), B(6,5) and C(1,4) be the vertices of
(1) The median from A meets BC at D. Find the coordinates of the points D.
(2) Find the coordinates of the points P on AD such that AP : PD = 2 : 1
(3) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RE = 2 : 1
(4) What do you observe ?
[Note : The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2 : 1 ]
(5) If are the vertices of find the coordinates of the centroid of the triangle
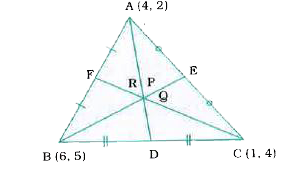
View SolutionLet (4, 2), B (6, 5) and C (1, 4) be the vertices of . :- The median from A meets BC at D. Find the coordinates of the point D.
View Solution