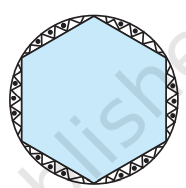
A round table cover has six equal designs as shown in figure. If the radius of the cover is 28 cm find the cost of making the designs at the rate of Rs.0.35 per cm2.[Use √3 = 1.7]
It can be observed that these designs are segments of the circle.Consider segment APB. Chord AB is a side of the hexagon. Each chord will substitute 360o/6 = 60o at the centre of the circle.In ΔOAB ∠OAB = ∠OBA As OA = OB∠AOB = 60°∠OAB + ∠OBA + ∠AOB = 180°2∠OAB = 180° − 60° = 120°∠OAB = 60°Therefore ΔOAB is an equilateral triangle.Area of ΔOAB == √3/4 x 282=196√3=196 x 1.7=333.2 cm2Area of sector OAPB = = 1/6 x 22/7 x 28 x 28 =1232/3 cm2Area of segment APB = Area of sector OAPB − Area of ΔOABTherefore area of designs = =2464-1999.2cm2= 464.8cm2Cost of making 1 cm2 designs = Rs 0.35Cost of making 464.76 cm2 designs = 464.8 x 0.35 =RS 162.68Therefore the cost of making such designs is Rs 162.68.
Related Solutions
A round table cover has six and equal designs, as shown in the figure. If the radius of the cover is cm find the cost of making the designs, at the rate of Rs. 0.35 per . [ Use ]
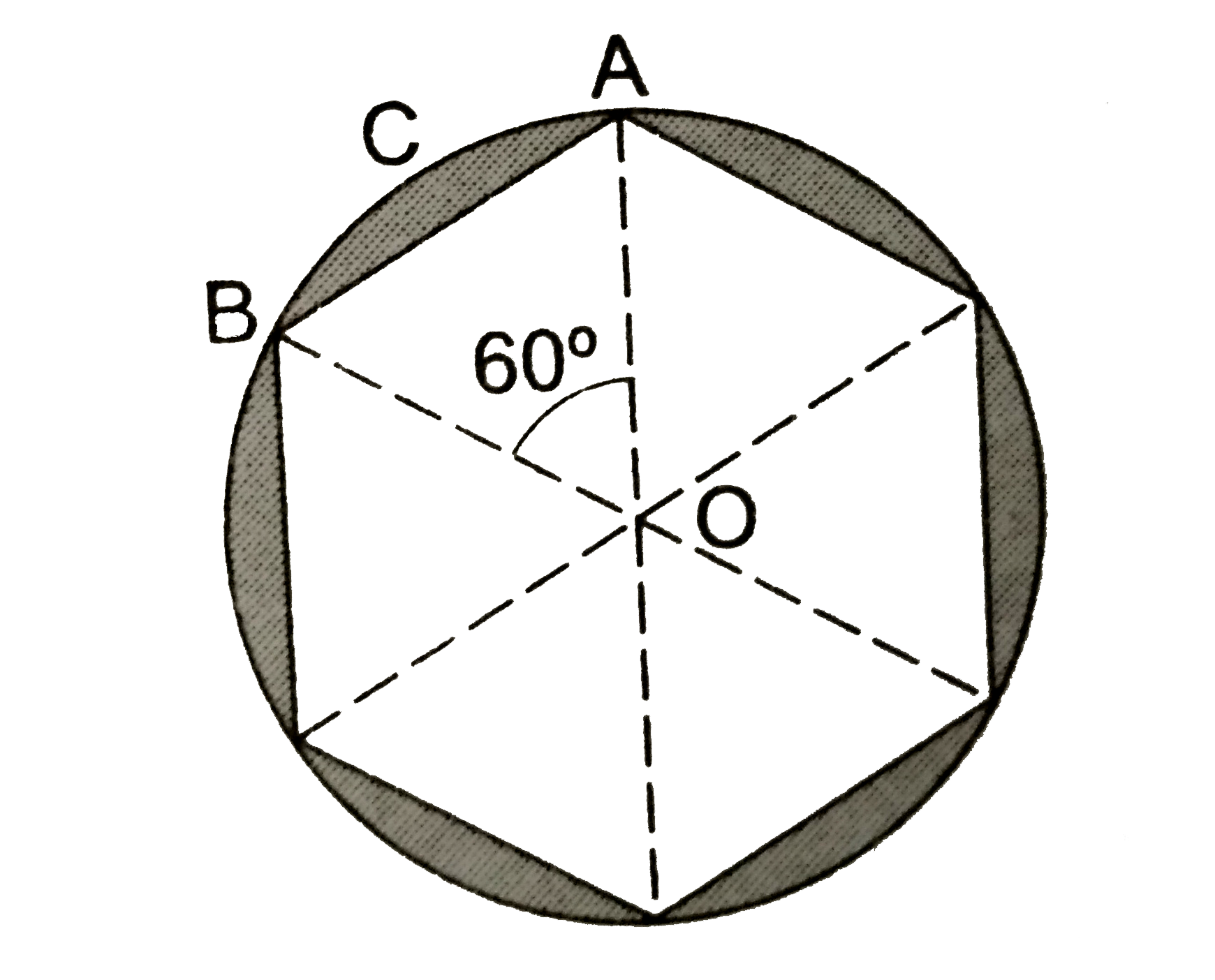
View SolutionA round table cover has six equal designs as shown in fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ? 0.35 per . (use
View SolutionA round table cover has six equal designs as shown in the given figure. If the radis of the cover is 28cm, find the cost of making the designs at the rate of Rs. 0.35 per . (Use )

View SolutionA round table cover has six equal designs as shown in Fig.12.14.
 If the radius of the cover is 28 cm,find the cost of making the designs at the rate of (use sqrt3=1.7)
If the radius of the cover is 28 cm,find the cost of making the designs at the rate of (use sqrt3=1.7)
View SolutionA round table cover has six equal designs as shown in Fig. 15.51. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs . (FIGURE)
View SolutionA round table cover has six designs of equal area as shown is the figure. If the radius of the cover is 28cm, find the cost of making the designs at the rate Rs.
View SolutionA round table cover has six equa designs as shown in Fig. 5.14. If the radius of the cover is 28 cm, find the cost of making the desingns at the rate of Rs 0.35 per
View SolutionCombination of polygon and Circle : A round table cover has 6 equal designs as shown in figure. If the radius of the cover is 28cm find the cost of making the designs at the rate of Rs. 0.35 per
View SolutionA round table cover has six equal designs as shown in the figure. If the radius of the cover is 28cm . Find the cost making the design at the rate of 3.50 per cm^2 .
View SolutionA round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is cm, find the cost of making the designs at the rate of .
View SolutionA round table top has six equal designs as shown in the figure. If the radius of the table top is , find the cost of making the designs with paint at the rate of per ( use

View SolutionA round table top has six equal designs as shown in the figure. If the radius of the table top is , find the cost of making the designs with paint at the rate of ( use
View SolutionA round table top has six equal designs as shown in the figure. If the radius of the table top is , find the cost of making the designs with paint at the rate of ( use
View SolutionConstruct a tangent to a circle of radius at any point .
View SolutionA round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of . (Use√ 3 = 1.7)
View SolutionA round table cover has six equal designs as shown in Fig. 15.51. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs . (FIGURE)
View SolutionA round table top has six equal diesigns as shown in the radius of the table top is 14 cm , find the cost of making the designs with point at the rate Rs 5 per . (Use
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use and ]

View Solutionएक गोल मेजपोश पर छः समान डिजाइन बने हुए है जैसाकि चित्र में दर्शाया गया है यदि मेजपोश की त्रिज्या 28 सेमी है तो Rs. 3.50 प्रति वर्ग सेंटीमीटर की दर से इन पर डिजाइनों को बनाने की लागत ज्ञात कीजिए ।

View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. (Use )
View Solution