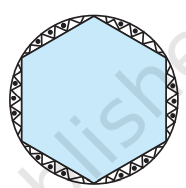
A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2.
We know that, in a circle with radius r and the angle at the center with degree measure θ,
(i) Area of the sector = θ360×πr2
(ii) Area of the segment = Area of the sector - Area of the corresponding triangle
Area of the design = Area of 6 segments of the circle.
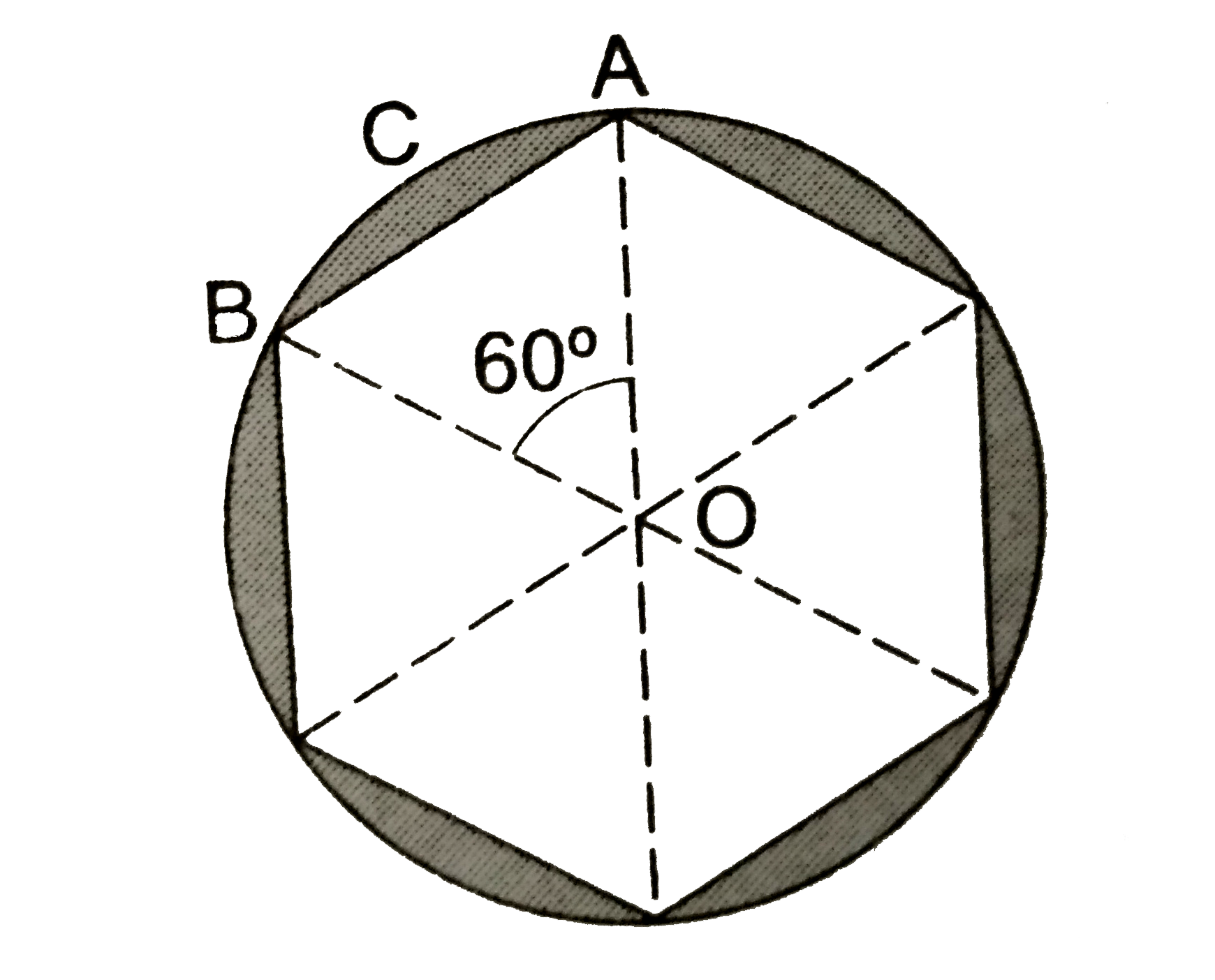
Since the table cover has 6 equal design, therefore angle of each sector at the center = 360∘6=60∘
Consider segment APB. Chord AB subtends an angle of 60∘ at the center.
Area of segment APB = Area of sector AOPB - Area of △AOB
Consider △AOB
OB=OA (radii of the circle)
∠OAB=∠OBA (angles opposite to equal sides in a triangle are equal)
∠AOB+∠OAB+∠OBA=180∘ (angle sum property of a triangle)
2∠OAB=180∘−60∘(Since,∠AOB=60∘)
∠OAB=120∘2=60∘
△AOB is an equilateral triangle
Area of △AOB=√34(side)2
=√34(28)2 (Since the side of the triangle = radii of the circle = 28 cm)
= √3×7×28
= 196√3
= 196×1.7
= 333.2cm2
Area of sector OAPB=60∘360∘×πr2
= 16×227×28×28
= 11×4×283
= 12323cm2
Area of segment APB = Area of sector OAPB - Area of △AOB
= (12323−333.2)cm2
Area of the designs = 6 × Area of segment
=6×(12323−333.2)cm2
= 2464−1999.2cm2
= 464.8cm2
Cost of making 1cm2 of designs = ₹ 0.35
Cost of making 464.8cm2of designs
= ₹ (0.35×464.8)
= ₹ 162.68
Similar Questions
A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2.

View SolutionCombination of polygon and Circle : A round table cover has 6 equal designs as shown in figure. If the radius of the cover is 28cm find the cost of making the designs at the rate of Rs. 0.35 per cm2
View SolutionA round table cover has six equal designs as shown in Fig. 15.51. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 3.50 per cm2 . (Use √3=1.7) (FIGURE)
View SolutionA round table cover has six and equal designs, as shown in the figure. If the radius of the cover is 28 cm find the cost of making the designs, at the rate of Rs. 0.35 per cm2. [ Use √3=1.7]
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. (Use √3=1.732andπ=3.14)
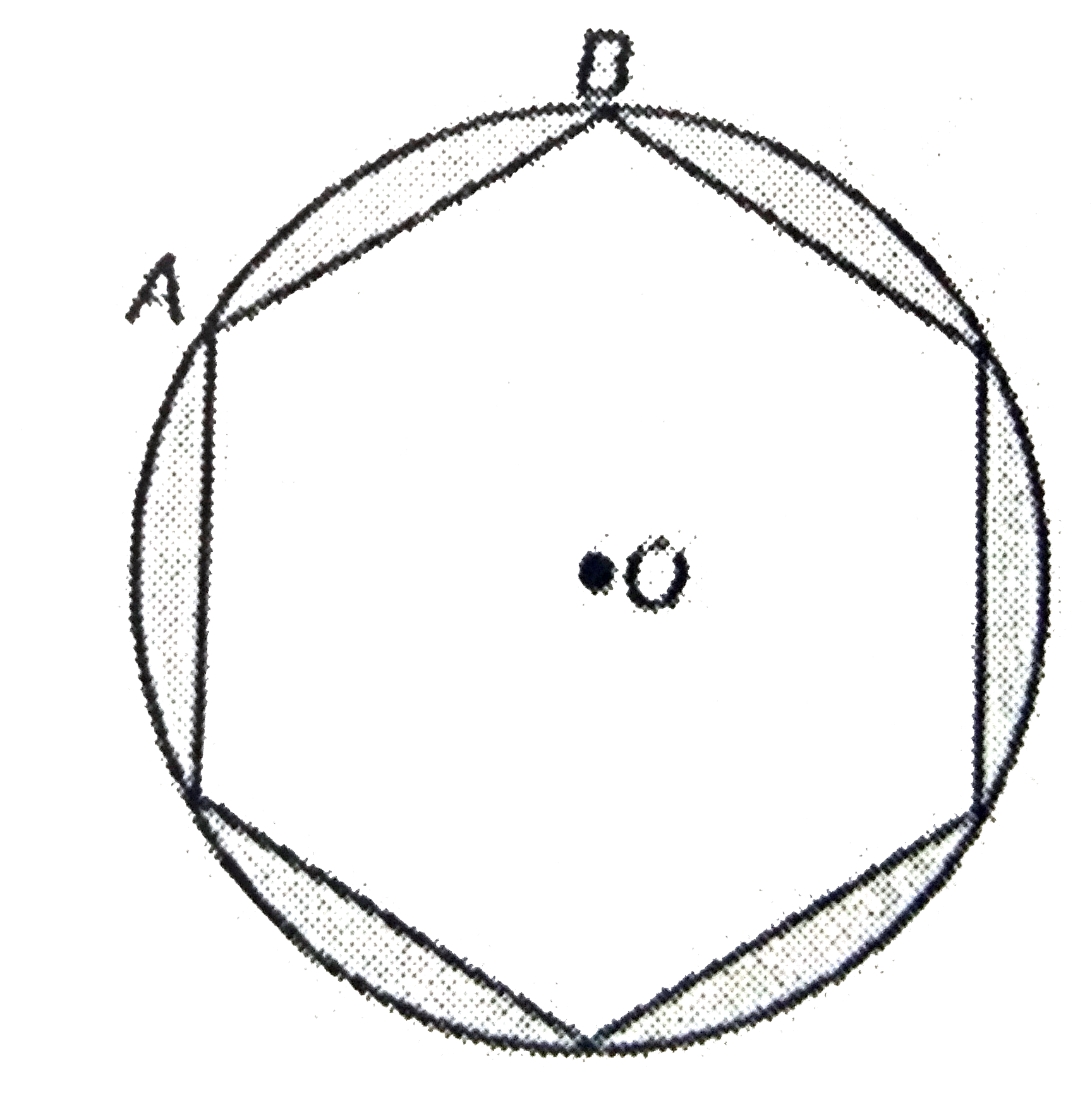
View SolutionA round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use √3=1.732 and π=3.14]

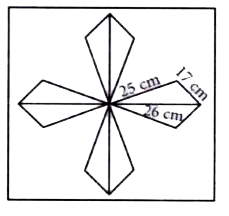
View SolutionA design is madeon a rectangular tile as shown in the given figure. The design has eight triangles, each of the side 25 cm, 17 cm and 26 cm. Find the total cost of making the design at the rate of 3.50 per cm2.
View SolutionA tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m, and slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of canvas of the tent at the rate of Rs 500 per m2 .
View SolutionA solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs 10 per dm2
View SolutionA bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of Rs 1.20 per cm2 .
View Solution
