A rotating disc Fig. 1.6 moves in the positive direction of the x axis. Find the equation y x describing the position of the instantaneous axis of rotation if at the initial moment the axis C of the disc was located at the point O after which it moved a with a constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration β the initial angular velocity is equal to zero;b with a constant acceleration ω and the zero initial velocity while the disc rotates counterclockwise with a constant angular velocity ω.
Rotating disc moves along the x-axis in plane motion in x-y plane. a motion of a solid can be imagined to be in pure rotation about a point say I at a certain instant known as an instantaneous center of rotation. The instantaneous axis whose positive sense is directed along vector ω of the solid and which passes through the point I is known as the instantaneous axis of rotation.Therefore the velocity vector of an arbitrary point P of the solid can be represented as:On the other hand x=vt wher x is the x cocrdinate of the C.M. Using this value of ω in Eq.b As center C moves with constant acceleration w with zero initial velocity
Related Solutions
A rotating disc moves in the positive direction of -axis as shown. Find the equation describing the position of the instantaneous axis of rotation if at the initial moment the centre of the disc was located at origin after which
a. it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity . b. it moved with constant velocity while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).
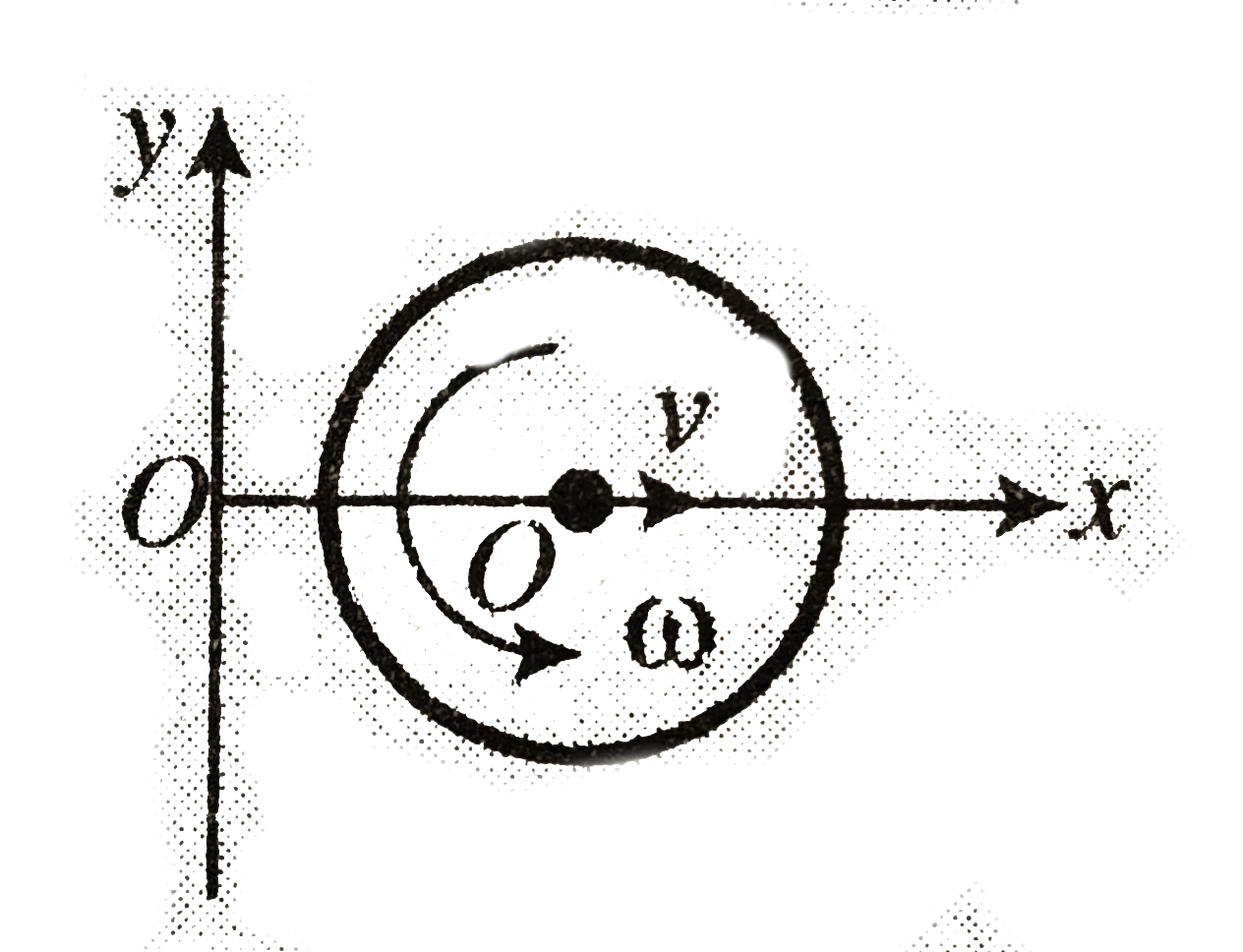
View Solution
A rotating disc moves in the positive direction of the x-axis. Find the equation describing the position of the instantaneous axis of rotation if at the initial moment of the centre of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration . the initial angular velocity is equal to zero.
View SolutionA rotating disc moves in the positive direction of the x-axis. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment of the centre c of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counterclockwise with a constant angular acceleration alhpa . the initial angular velocity is equal to zero.
View SolutionA horizontal disc rotates with a constant angular velocity omega=6.0rad//s about a vertical axis passing through its centre. A diameter of the disc with a velocity v^'=50cm//s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.
View SolutionA disc rotates about its axis with a constant angular acceleration of . Find the radia and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA disc rotates about its axis with a constant angular acceleration of . Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA disc rotates about its axis with a constant angular acceleration of . Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA circular disc is rotating about its own axis at constant angular acceleration. If its angular velocity increases from 210 rpm to 420 rpm during 21 rotations then the angular acceleration of disc is
View SolutionA disc of moment of inertia la is rotating in a horizontal plane about its symmetry axis with constant angular speed co. Another discinitially at rest of moment of inertia I, is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed The loss of kinetic energy due to friction in this process is,
View SolutionA circular disc of moment of inertia is rotating in a horizontal plane about its symmetry axis with a constant angular velocity . Another disc of moment of inertia is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed . Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA circular disc of moment of inertia I_(t) is rotating in a horizontal plane about its symmetry axis with a constant angular velocity omega_(i) . Another disc of moment of inertia I_(b) is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed omega_(f) . Calculate the energy lost by the initially rotating disc due to friction.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is in each case.

View SolutionA constant power is supplied to a rotating disc. The relationship of angular velocity (w) of disc and number of rotations (n) made by the disc is govermed by
View SolutionA constant power is supplied to a rotating disc. The relationship of angular velocity (w) of disc and number of rotations (n) made by the disc is governed by:
View SolutionA disc, initially at rest, starts rotating about its own axis/ with a constant angular acceleration of 0*2 rad/s2. The time taken by the disc to rotate by 10 rad (in seconds) is
View SolutionMoment of inertia of a disc about the axis of rotation is 10 kgm^2 . A constant torque of 50 Nm acts on it. Find :Angular velocity at the end of 10s, if the disc is initially at rest.
View Solutionजड़त्व आघूर्ण की एक वृत्ताकार डिस्क अपनी सममिति अक्ष के परितः, एक स्थिर कोणीय वेग से क्षैतिज तल में घूर्णन कर रही है। इस डिस्क के ऊपर जड़त्व आघूर्ण की एक अन्य डिस्क संकेन्द्री डाल दी जाती है। प्रारंभ में दूसरी डिस्क की कोणीय चाल शून्य है। अन्ततः दोनों डिस्क एक ही स्थिर कोणीय वेग से घूर्णन करने लगती हैं। प्रारंभ में घूर्णन करती हुई डिस्क की घर्षण के कारण नष्ट हुई ऊर्जा है ।
View SolutionA disc of radius 10 cm is rolling on a horizontal surface. The velocity of its centre is and angular velocity of rotation of the disc is . What is the distance (in cm) of instantaneous axis of rotation from the centre of the disc ?
View SolutionA circular disc of moment of inertia is rotating in a horizontal plane, about its symmetry axis, with a constant angular speed . Another disc of moment of inertia is placed coaxially on the rotating disc. Initially the second disc has zero angular speed. Eventually both the discs rotate with a constant angular speed . The energy lost by the initially rotating disc to friction is ............
View Solution