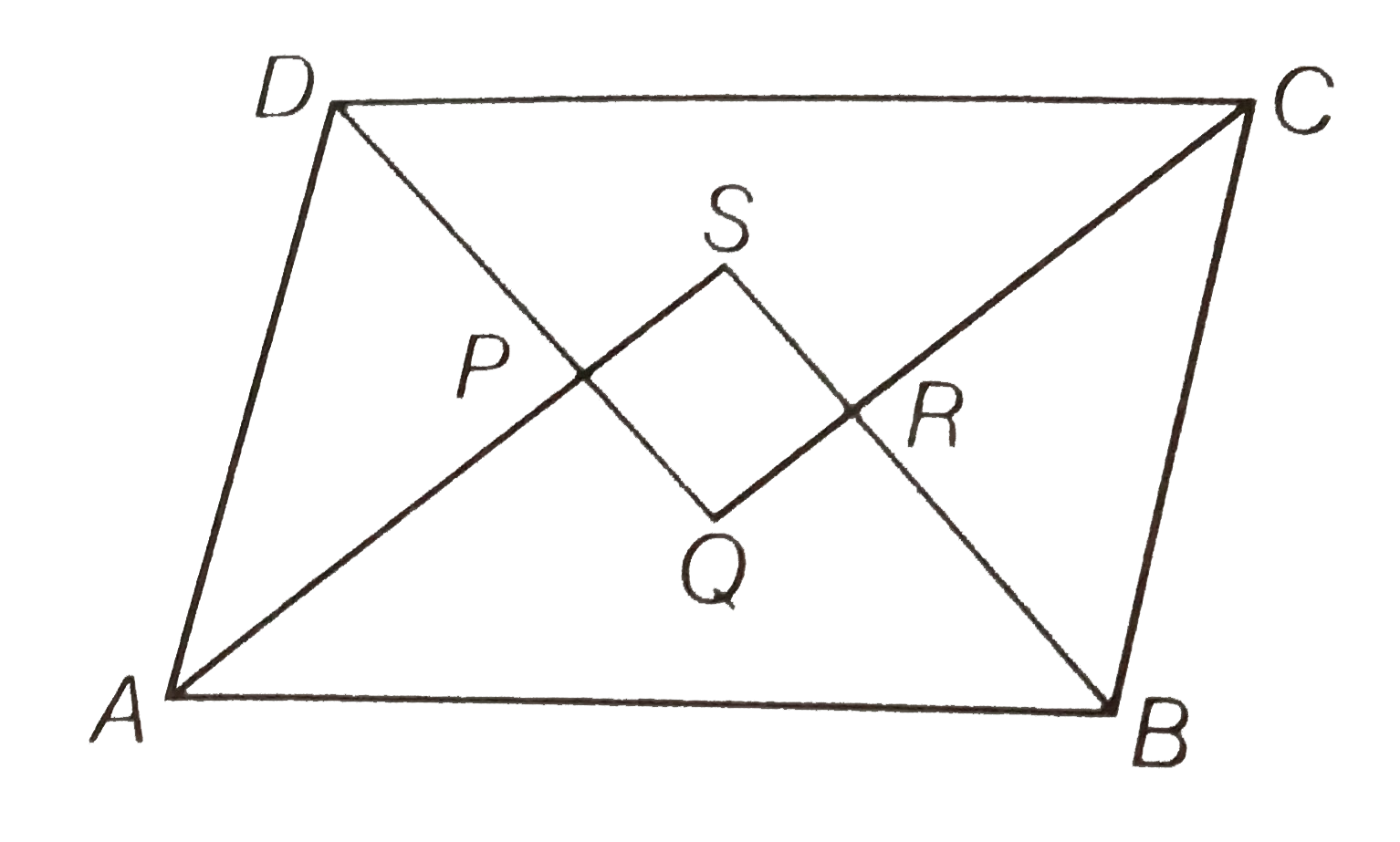
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
ABCD is a cyclic quadrilateral. Its angle bisectors from a quadrilateral PQRS.To Prove : PQRS is a cyclic quadrilateral.Proof : ∠1 + ∠2 + ∠3 = 1800 ...i [∵ Sum of the angles of a D is 1800] ∠4 + ∠5 + ∠6 = 1800 ...ii [∵ Su m of the angles of a D is 1800] ∴∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360.. ....iii [Adding i and ii] But ∠2 + ∠3 + ∠6 + ∠= 1/2[∠A + ∠B + ∠C +∠D] = 1/2.3600 = 1800 [∵Sum of the angles of quadrilateral is 3600] ∴ ∠1 + ∠4 = 3600 - ∠2 + ∠3 + ∠6 + ∠5 ∴ PQRS is a cyclic quadrilateral. [∵ If the sum of any pair of opposite angles of a quadrilateral is 1800 then the quadrilateral is a cyclic] Hence Proved.
Related Solutions
Prove that the quadrilateral formed by the bisectors of the angles of a cyclic quadrilateral is also cyclic.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a cyclic quadrilateral is cyclic.
View SolutionProve that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic
View SolutionThe quadrilateral formed by the bisectors of the angles of a parallelogram is a
View Solutionसिद्ध कीजिए कि एक चतुर्भुज के कोणों को समद्विभाजित करने से बना चतुर्भुज चक्रीय होता है |
View SolutionProve that the bisectors of the four angles of quadrilateral produce jointly a cyclic quadrilateral.
View SolutionThe quadrilateral formed by the bisectors of the angles of a parallelogram is a

View SolutionProve that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
View SolutionProve that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
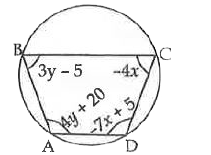
View SolutionABCD is a cyclic quadrilateral. Find the angle A of the cyclic quadrilateral.
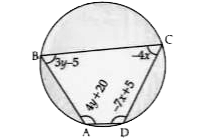
View SolutionABCD Find the angles of a cyclic quadrilateral cyclic quadrilateral.
View SolutionABCD is a cyclic quadrilateral. Find the angles of the cyclic quadrilateral.
View SolutionABCD is a cyclic quadrilateral. Find the angles of the cyclic quadrilateral.
View Solutionसिद्ध कीजिए की किसी चतुर्भुज के अंत : कोणों के अर्द्धको (कोण समद्विभाजको) से बना चतुर्भुज चक्रीय होता है।
View SolutionProve that the bisectors of the angles formed by producing the opposite sides of a cyclic quadrilateral (provided that they , are not parallel), intersect at right angles.
View SolutionAnswer any one question : Prove that the quadrilateral foemed by the internal bisectors of the four angles of a quadrilateral is cyclic.
View Solution