Let ABC be an acute angled triangle. The circle Γ with BC as diameter intersects AB and AC again at P and Q respectively. Determine ∠BAC given that the orthocenter of triangle APQ lies on Γ.
Let K denote the orthocenter of triangle APQ. Since triangles ABC and AQP are similar it follows that K lies in the interior of triangle APQ. Note that ∠KPA = ∠KQA = 900 - ∠A. Since BPKQ is a cyclic quadrilateral it follows that ∠BQK = 1800 - ∠BPK = 900 - ∠A while on the other hand ∠BQK = ∠BQA - ∠KQA = ∠A since BQ is perpendicular to AC. This shows that 900 - ∠A = ∠A so ∠A = 450.
Related Solutions
In an acute angled the circle on altitude AD as diameter cuts AB at P and AC at Q then PQ
View SolutionABC is a triangle, P is a point on AB and Q is a point on AC such that . Complete the (.... relation .
View SolutionIn acute-angled triangle ABC, AD is the altitude, Circle drawn with AD as its diameter cuts the AB and AC at P and Q, respectively. Length PQ is equal to
View SolutionIn circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionIn ABC, right-angled at B, AB = 3 cm and BAC . Determine the lengths of the sides BC and AC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
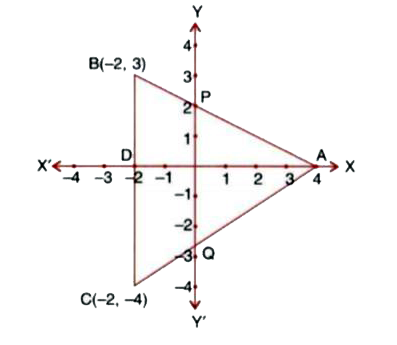
Find the length of AB and AC.
View SolutionIn triangle ABC, the line PQ is drawn parallel to BC while the points P, Q are on AB and AC respectively. If AB = 3AP, then what is the ratio of area of triangle APQ to that of triangle ABC?
View Solutionबिंदु P और Q क्रमश : त्रिभुज ABC की भुजा AB और BC पर स्थित हैं, त्रिभुज B पर समकोण है
View SolutionIn the below given figure P and Q are points on the sides AB and AC respectively of such that AQ = 3cm, QC= 5cm and . Find the ratio of areas and .
View SolutionAltitude AD of an equilateral triangle ABC is a diameter of circle. If circle intersect AB and AC at E and F then =
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to
View SolutionIn a right triangle ABC, a circle with a side AB diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right-triangle ABC in which , a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
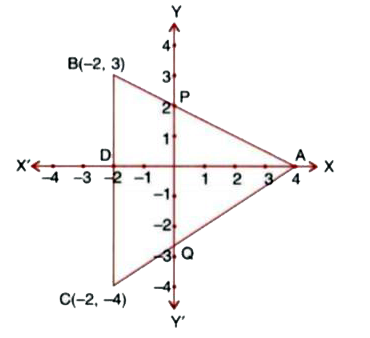
Find the equation of the line AC.
View SolutionIn an isoceles triangle ABC, the acute angle BAC is Point D lies on such that is the angle bisector of . Find .
View SolutionPoints P and Q lie on sides AB and AC of triangle ABC respectively such that segment PQ is parallel to side BC. If the ratio of areas of triangle APQ: triangle ABC is 25 : 36, then the ratio PA : PB is
View Solution