Consider regular polygons with number of sides n = 3 4 5.... as shown in the figure. The center of mass of all the polygons is at height h from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is Δ. Then Δ depends on n and h as
Related Solutions
Consider regular polygons with number of sides n = 3, 4, 5 ...... as shown in the figure, The center of mass of all the polygons is at height h from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted,. The maximum increase in height of the locus of the center of mass for each polygton is . Then depends on n and h as
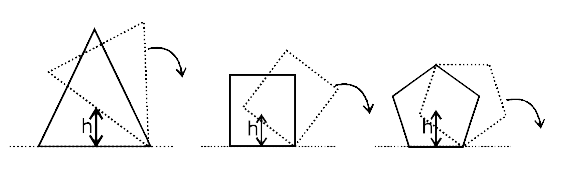
View SolutionConsider regular polygons with number of sides n = 3, 4, 5 ...... as shown in the figure, The center of mass of all the polygons is at height h from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted,. The maximum increase in height of the locus of the center of mass for each polygton is Delta . Then Delta depends on n and h as
View Solutionचित्र द्वारा दर्शाये संबहुभुजाओं की संख्या n = 3,3,5 ..... है । सभी बहुभुजाओं का संहित केंद्र अनुभूमिक तल से h ऊंचाई पर है । बिना फिसले क्षैतिज तल पर प्रतिगामी शीर्ष के चारों ओर घूर्णन कर अर्गसृत हो रहे हैं । प्रत्येक बहुभुज के संहित केंद्र के रेखापाठ की ऊंचाई की अधिकतम वृद्धि है । तब की h और n पर निर्भरता निम्न में से दी जायगी -
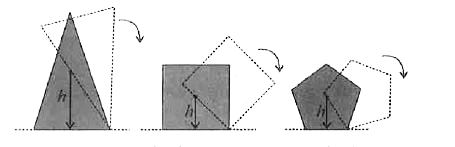
View Solutionचित्र द्वारा दर्शाये समबहुभुजों की भुजाओं की संख्या n=3, 4, 5......... है। सभी बहुभुजों का संहति केन्द्र (center of mass) अनुभूमिक तल से hऊँचाई पर है। ये बिना फिसले क्षितिज तल पर प्रतिगामी शीर्ष (leading vertex) के चारों ओर घूर्णन कर अग्रसरित हो रहे है। प्रत्येक बहुभुज के संहति केन्द्र के रेखापथ (locus) की ऊँचाई की अधिकतम वृद्धि हैं तब की h और n पर निर्भरता निम्न में से दी जाएगी।

View Solutionn भुजाओं वाले बहुभुज के शीर्षो पर समान द्रव्यमान (m) के (n-1) बिंदु द्रव्यमान स्थित है। बहुभुज के द्रव्यमान केंद्र से खाली शीर्ष का स्थिति सदिश है द्रव्यमान केंद्र का धनात्मक सदिश होगा
View Solutionकिसी नियमित n- बहुभुज के शीर्षों पर m द्रव्यमान के (n-1) समान बिंदु द्रव्यमान स्थित हैं। इसके खाली शीर्ष का बहुभुज के केंद्र के सापेक्ष स्थिति सदिश a है। द्रव्यमान केंद्र की स्थिति सदिश ज्ञात कीजिए।
View Solution(n-1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector with respect to the center of the polygon. Find the position vector of centre of mass.
View Solutionएक वृत्त के अंतर्गत संबहुभुज खींचा गया है। संबहुभुज की प्रत्येक भुजा केंद्र पर का कोण अंतरित करती है, तो संबहुभुज की भुजाओं की संख्या ज्ञात कीजिए।
View Solutionm द्रव्यमान के (n-1) समान बिन्दु पर द्रव्यमान n- बहुभुज वाले नियमित शीर्षों पर रखे गए हैं। खाली शीर्षों के बहुभुज के केन्द्र के सापेक्ष स्थिति सदिश a है। यदि n=7 हो, तो द्रव्यमान केन्द्र का स्थिति सदिश क्या होगा?
View SolutionA polygon is a regular polygon if all its sides are equal.
View SolutionAn exterior angle of a regular polygon having sides is more than that of the polygon having sides by . Then find the number of the sides of each polygon
View SolutionWhat is a regular polygon?State the name of a regular polygon of: (a) 3 sides (b) 4 sides (c)5 sides.
View Solutionregular polygon is 1080^(@) then number of sides in the polygon is
View SolutionEach interior angle of a regular polygon is 144^@ . The number of sides of the polygon is:
View Solutioneach interior angle of a regular polygon 144^@ Is. The number of sides in the polygon is
View SolutionIf each interior angle of regular polygon is 144^(@) then what is the number of sides in the polygon
View SolutionRegular polygon a polygon is called a regular polygon if all its sides are equal and all its angles are equal.
View SolutionA circle of radius r is inscribed in a regular polygon with n sides (the circle touches all sides of the polygon). If the perimeter of the polygon is p, then the area of the polygon is
View SolutionIn an n-sided regular polygon, each interior angle is . Find the number of the sides of the polygon.
View SolutionIn an n-sided regular polygon, each interior angle is . Find the number of the sides of the polygon.
View Solution