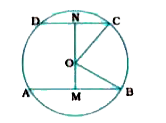
he lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre what is the distance of the other chord from the centre?
Let PQ and RS be two parallel chords of a circle with centre O. We have PQ = 8 cm and RS = 6 cm. Draw perpendicular bisector OL of RS which meets PQ in M. Since PQ || RS therefore OM is also perpendicular bisector of PQ. Also OL = 4 cm and RL = 1/ 2 RS ⇒ RL = 3 cm and PM = 1/ 2 PQ ⇒ PM = 4 cm In ∆ORL we have OR2 = RL2 + OL2 [Pythagoras theorem]⇒ OR2 = 32 + 42 = 9 + 16 ⇒ OR2 = 25 ⇒ OR = 25 ⇒ OR = 5 cm ∴ OR = OP [Radii of the circle] ⇒ OP = 5 cm Now in ∆OPM OM2 = OP2 – PM2 [Pythagoras theorem] ⇒ OM2 = 52 – 42 = 25 – 16 = 9 OM = 9 = 3 cm Hence the distance of the other chord from the centre is 3 cm. Ans.
Related Solutions
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chords is at distance 4 cm from the centre, what is the distance of the other chord from the centre ?
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre ?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionLength of two chords of a circle with centre at O are 6 cm and 8 cm. If the length from centre to the smaller chord is 4 cm then find the distance from centre of the greater chord.
View SolutionA chord 6 cm long is at a distance of 4 cm from the centre of a circle. Find the length of a chord which is at a distance of 3 cm from the centre of the circle.
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionThe length of two parallel chords of a circle are and If the smaller chord is at a distance of from the centre, what is the distance of the other chord from the centre?
View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
View SolutionIf the length of a chord of a circle is 48 cm and the distance of this chord from the centre is 7 cm , then find the length of the chord , the distance of which form the centre is 20 cm.
View SolutionRadius of circle is 10 cm. There are two chords of length 16 cm each. What will be the distance of these chords from the centre of the circle ?
View SolutionThe distances of two chords AB and CD from the centre of a circle are 6 cm and 8 cm respectively. Then, which chord is longer?
View SolutionThe distances of two chords AB and CD from the centre of a circle are 6 cm and 8 cm respectively. Then, which chord is longer?
View SolutionLengths of two parallel chords of a circle are 6cm and 8cm. If the smaller chord is at a distance of 3sqrt(3)cm from the centre of the circle,then the distance of the larger chord from the centre of the circle would be
View Solution17 cm. A chord in a circle of radius 8 cm from the centre. Is at a distance of. What is the length of the chord?
View SolutionThe length of diameter in a circle is 10 cm. If the distance from centre to chord of this circle is 4 cm, then find the length of this chord.
View SolutionRadius of a circle is 5 cm. The length of a chord of the circle is 8 cm. Find the distance of the chord from the centre.
View SolutionDistance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of the circle.
View SolutionThe chord of a circle of radius 5 cm is of length 8 cm. The distance of the chord from the centre of the circle
View Solution