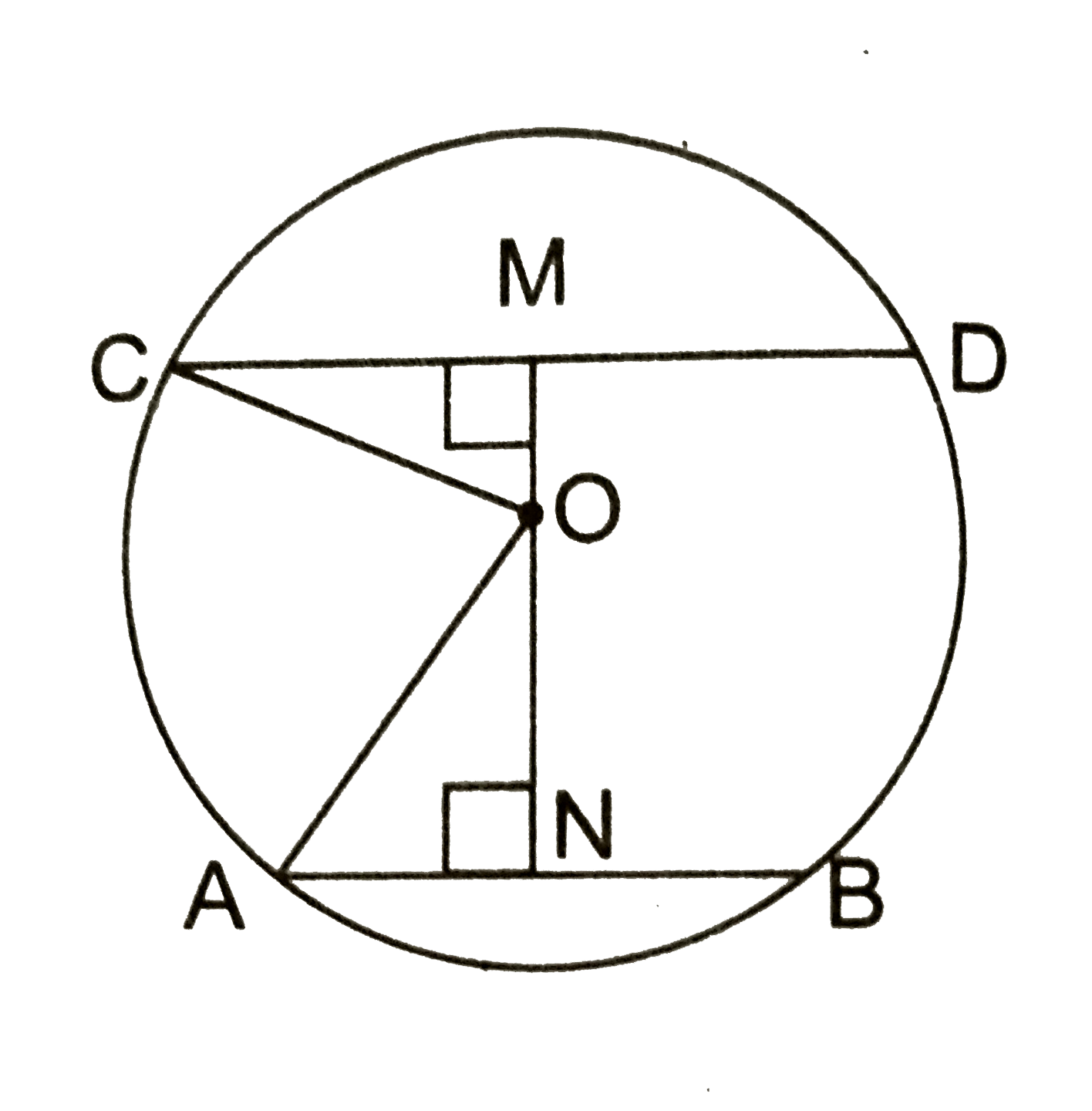
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm find the radius of the circle.
Let O be the centre of the circle and let its radius be r cm. Draw OM ⊥ AB and OL ⊥ CD. Then AM = 1/ 2 AB = 5/ 2 cm and CL = 1/ 2 CD = 11/ 2 cm Since AB || CD it follows that the points O L M are 10 CIRCLES collinear and therefore LM = 6 cm. Let OL = x cm. Then OM = 6 – x cm Join OA and OC. Then OA = OC = r cm. Now from right-angled ∆OMA and ∆OLC we have OA2 = OM2 + AM2 and OC2 = OL2 + CL2 [By Pythagoras Theorem] ⇒ r2 = 6 – x2 + 5/ 2 2 ..i and r2 = x2 + 11/ 2 2 ... ii⇒ 6 – x2 + 5/ 2 2 = x2 + 11/ 2 2 [From i and ii] ⇒ 36 + x2 – 12x + 25/ 4 = x2 + 121/ 4 ⇒ – 12x = 121/ 4 – 25/ 4 – 36 ⇒ – 12x = 96/ 4 – 36 ⇒ – 12x = 24 – 36 ⇒ – 12x = – 12 ⇒ x = 1Substituting x =1 in i we get r2 = 6 – x2 + 5/ 2 2 ⇒ r2 = 6 – 12 + 5/ 2 2 ⇒ r2 = 52 + 5/ 2 2= 25 + 25/ 4 ⇒ r2 = 125/ 4 ⇒ r = 5 5 2 Hence radius r = 5 5 2 cm. Ans.
Related Solutions
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of length 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.

View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionAB and CD are two chords of a circle where AB = 10 cm, CD = 24 cm and AB||CD. Distance between AB and CD is 17 cm. Find the radius of the circle. (The chords are located on opposite sides of the centre)
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionIn a circle with centre O. AB and CD are parallel chords lying on opposite sides of a diameter parallel to them. If AB = 30 cm, CD - 48 cm and the distance between AB and CD is 27 cm, find the radius of the circle.
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that , and the distance between AB and CD is . Find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that , and the distance between AB and CD is . Find the radius of the circle.
View Solutionand are two parallel chords of a circle such that and If the chords are on the opposite sides of the centre and the distance between them is find the radius of the circle.
View Solutionएक वृत्त की 5 सेमी तथा 11 सेमी लम्बी दो जीवाएं AB और CD समांतर है और केंद्र की विपरीत दिशा में स्थित है। यदि AB और CD के बीच की दूरी 6 सेमी हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त की 5 cm तथा 11 cm लम्बी दो जीवाऍ AB और CD समान्तर है और केंद्र की विपरीत दिशा में स्थित है । यदि AB और CD के बीच की दूरी 6 cm हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त की 5 cm तथा 11 cm लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्र की विपरीत दिशा में स्थित हैं | यदि AB और CD के बीच की दूरी 6 cm हो, तो वृत्त की त्रिज्या ज्ञात कीजिए |
View Solutionकेंद्र O वाले वृत्त में, AB और CD व्यास के एक ही पक्ष में दो समानांतर जीबाएं हैं। यदि AB = 12 cm, CD 18 cm और जीवाओं AB और CD के बीच की दूरी 3 cm है, तो वृत्त की विज्या (cm में) जात करें।
View Solution