A particle of unit mass is moving along the x-axis under the influence of a force and its total energy is conserved. Four possible forms of the potential energy of the particle are given in column I a and U0 are constants. Match the potential energies in column I to the corresponding statements s in column II.Column-IColumn-IIAU1x=U0/2 [1-x/a2]2pthe force acting on the particle is zero atx = aBU2x=U0/2x/a2Qthe force acting on the particle is zero atx = 0.CU3x=U0/2x/a2 exp [-x/a2] Rthe force acting on the particle is zero at x= – aDU4x=U0/2[x/a-1/3x/a3]SThe particle experiences an attractive force towards x = 0 in the region |x|
Answer:A→P Q R T B→Q S C→P Q R S D→P R T
Related Solutions
A particle of unit mass is moving along the x-axis under the influence of a force and its total energy is conserved. Four possible forms of the potential energy of the particle are given in column-I (a and U0 are constants). Match the potential energies in column-I to the corresponding statement(s) in column-II. {:((A),U_1(x)= (U_0)/(2)[1-(x/a)^(2)]^(2),(P),"the force acting on the particle is zero at x = a."),((B),U_2(x)= (U_0)/(2)(x/a)^(2),(Q),"the force acting on the particle is zero at x = 0."),((C),U_2(x)= (U_0)/(2)(x/a)^(2)exp[-(x/a)],(R),"the force acting on the particle is zero at x = 0."),((D),U_4(x)= (U_0)/(2)[x/a - 1/3 (x/a)^3],(S),"The particle experiences an attractive force towards x = 0 in the region | x | < a"),(,,(T),"The particle with total energy" (U_0)/4 " can oscillate about the point"x = -a.):}
View Solutionइकाई द्रव्यमान का एक कण एक बल के प्रभाव में x-अक्ष पर गति कर रहा है । कण की जूल ऊर्जा संरक्षित है। कॉलम-I में कण की स्थितिज उर्जाओ के चार संभावित रूप दिए गए है (a तथा स्थिरांक है)। कॉलम- I में दी गयी स्थितिज उर्जाओ का कॉलम- II में दिए गए कथन/कथनो से उचित मिलान कीजिये ।

View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[(x^(2))/(2)-x]J . If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x) =(x^(2)/2-x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View SolutionIn figure, the variation of potential energy of a particle of mass is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
View SolutionIn figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:
View SolutionThe potential energy of a particle under a conservative force is given by J. The equilibrium position of the particle is at
View SolutionThe potential energy of a particle under a conservative force is given by U ( x) = ( x^(2) -3x) J. The equilibrium position of the particle is at
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as Joule where x is in meter. Then:
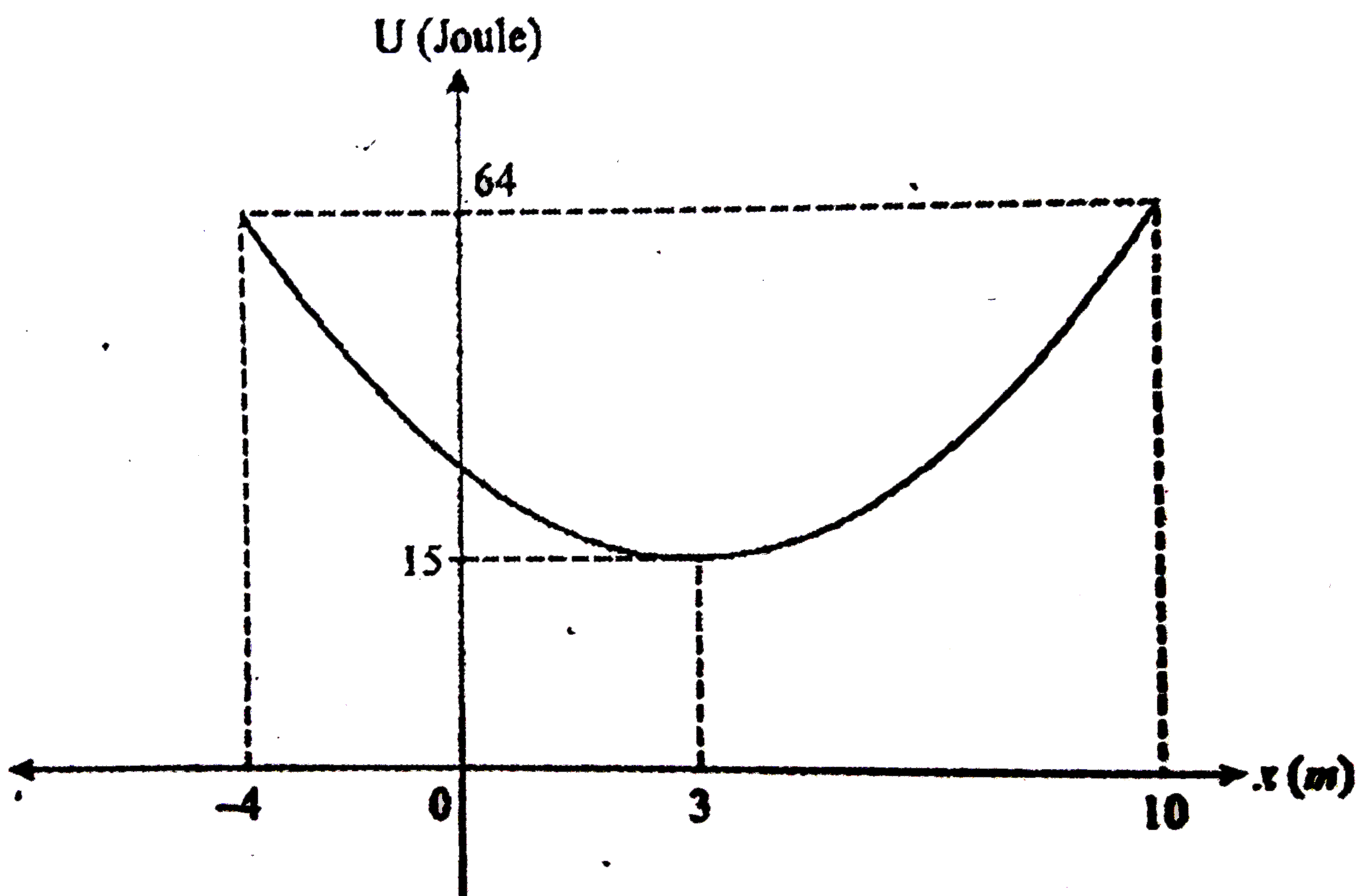
View SolutionAs a particle moves along the x- axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
View SolutionAs a particle moves along the x- axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
View SolutionAs a particle moves along the x- axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
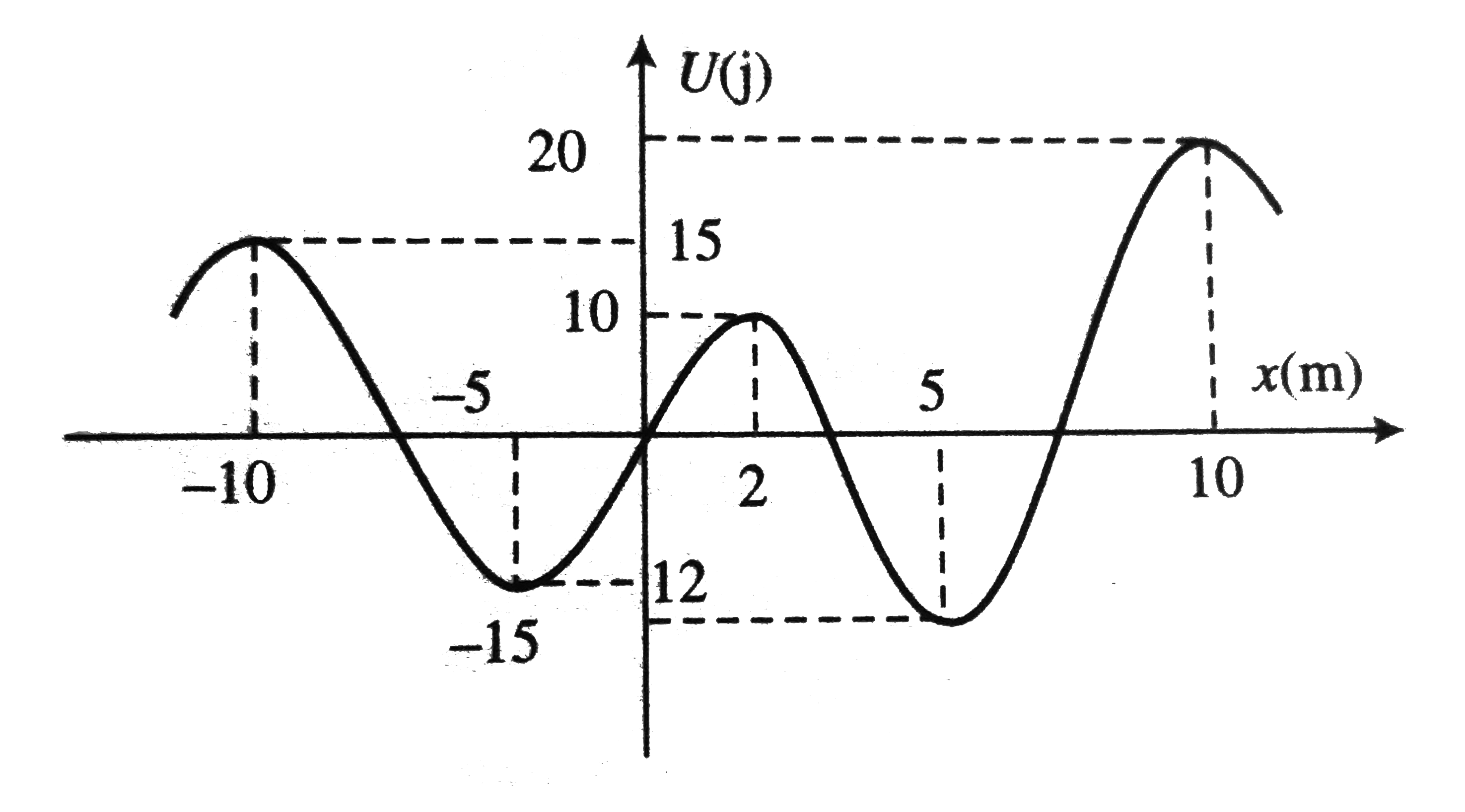
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
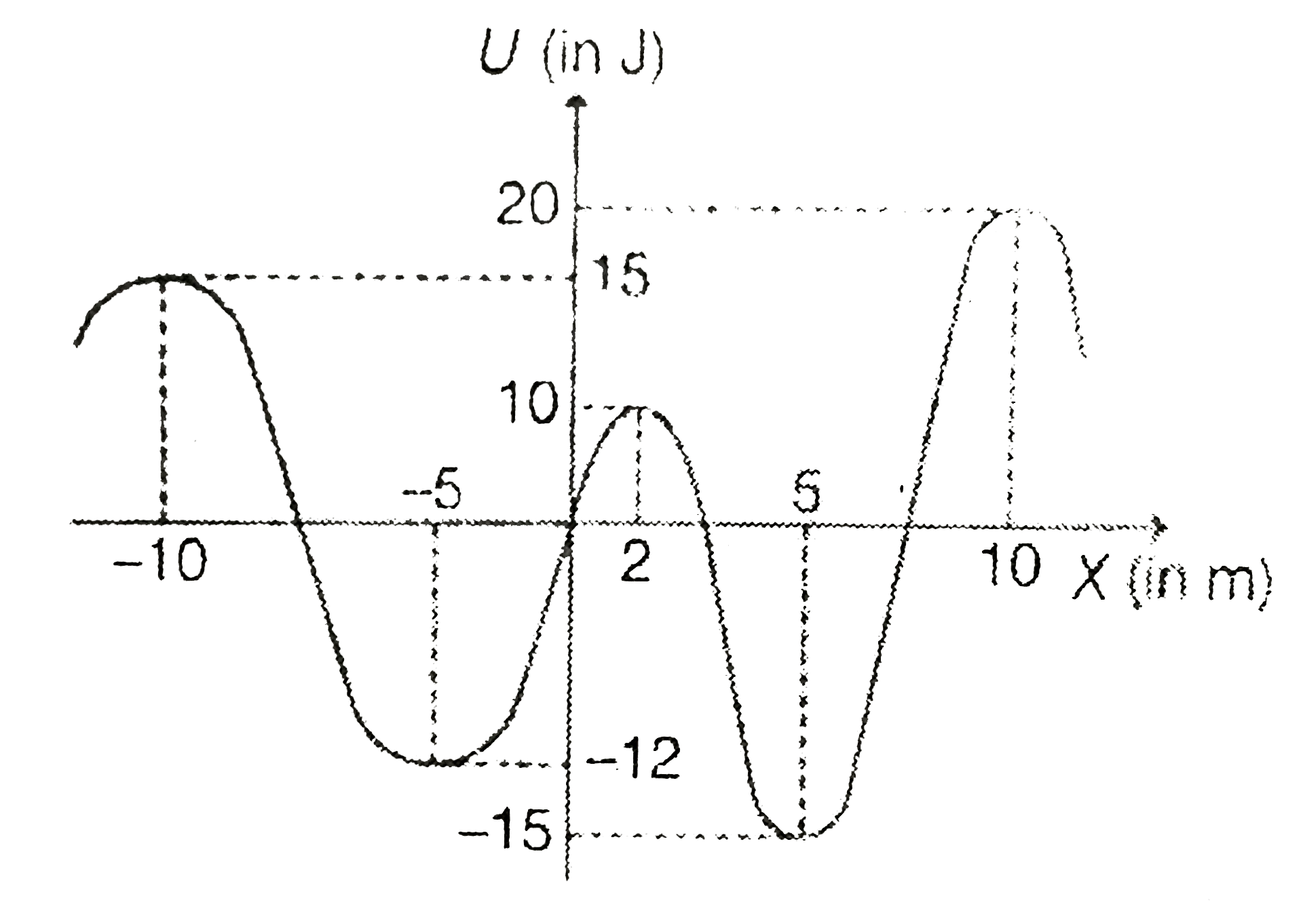
If the particle is released at the origin, then
View SolutionIn the figure the variation of potential energy of a particle of mass is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
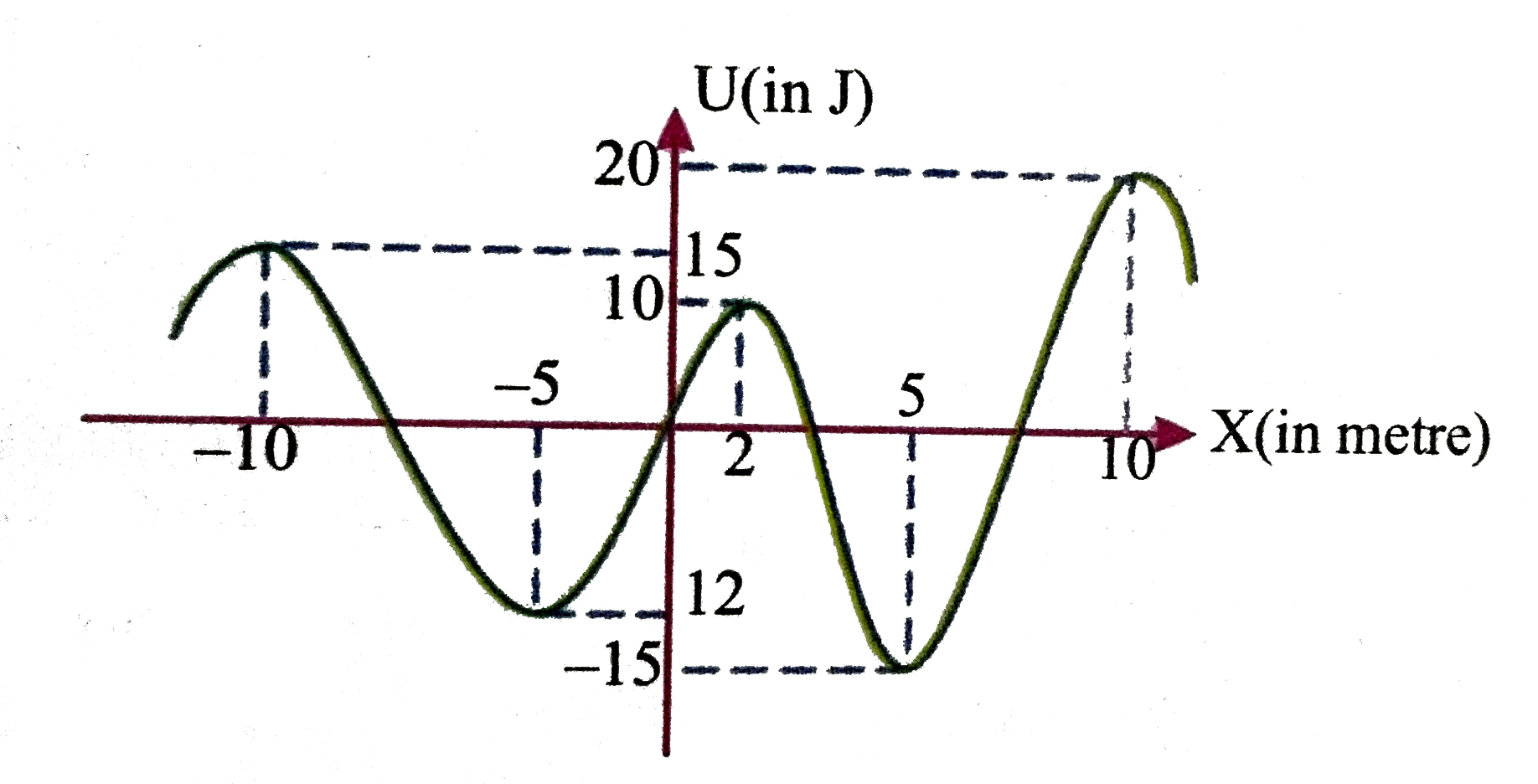
If the particle is released at the origin then
View SolutionIf x, F and U denote the displacement force acting on and potential energy of a particle:
View SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View SolutionA conservative force F(x) act on a 1kg particle. The potential energy U(x)=(x-4)^(2) , At x=5 ,particle has kinetic energy of 24J .The greatest value of x to which particle can move is
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
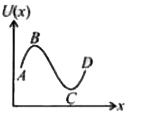
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
View Solution