Two strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB The ratio vA /vB is a 1/2 b 2 c 1/4 d 4.
The correct answer is a 1/2EXPLANATION: The velocity of the wave on a string is v = √F/µ where µ = mass per unit length. So the velocity is inversely proportional to the square root of the mass per unit length of the string. Here the µₐ/µᵦ = 4πr²/πr² =4 Hence vₐ/vᵦ = √µᵦ/µₐ =√1/4 = 1/2
Related Solutions
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. Atransverse wave travels on A with speed vA and on B with speed . The ratio is:
View SolutionTwo strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed with speed . The ratio is
View SolutionTwo strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed and on B with speed . The ratio is
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed and on B with speed . The ratio is
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed and on B with speed . The ratio is
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed and on B with speed . The ratio is
View SolutionTwo strings A and B made of same material are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed and on B with speed . The ratio is
View Solutionसमान पदार्थ की दो डोरियाँ A तथा B समान तनाव से खींची, जाती है | डोरी A की त्रिज्या डोरी B की त्रिज्या से दोगुनी है | एक अनुप्रस्थ तरंग A पर चाल से तथा B पर चाल से चलती है | एवं का अनुपात है
View SolutionLet A and B be two points on a parabola y^2 = x with vertex V such that VA is perpendicular to VB and theta is the angle between the chord VA and the axis of the parabola. The value of (|VA|)/(|VB|) is
View SolutionLet A and B be two points on a parabola y^(2)=x with vertex V such that VA is perpendicular to VB and theta is the angle between the chord VA and the axis of the parabola.The value of (|VA|)/(|VB|) is
View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View SolutionTwo strings of same material are stretched to the same tension . If their radii are in the ratio 1:2 , then respective wave velocities in them will be in ratio
View SolutionThe speed of a transverse wave in a stretched string is 348 ms^(-1) , when the tension of the string is 3.6 kg wt. Calculate the speed of the transverse wave in the same string . If the tension in the string is changed to 4.9 kg wt ?
View Solutionदो डोरियाँ A तथा B के ही पदार्थ की बनी हैं तथा उनमें तनाव भी एक जितना ही है । A की त्रिज्या की B त्रिज्या से दुगुनी है । एक अनुप्रस्थ तरंग, A पर चाल से तथा B पर चाल से चलती है । का मान होगा
View SolutionThe potential difference (VA – VB) between the points A and B in the given figure is
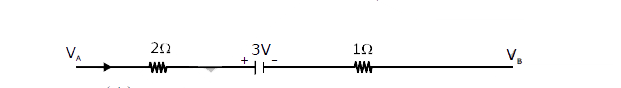
View SolutionSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View SolutionSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View SolutionSpeed of transverse wave on string is v . If tension is increased by factor of 4 and radius of the string is increased by factor of 2, then the new wave speed will be :
View SolutionA string of length I is stretched by II 30 and transverse waves in the string are found to travel at a -speed v_0 . Speed of transverse waves when the string is stretched by II15 will be :
View SolutionTwo strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is
View Solution