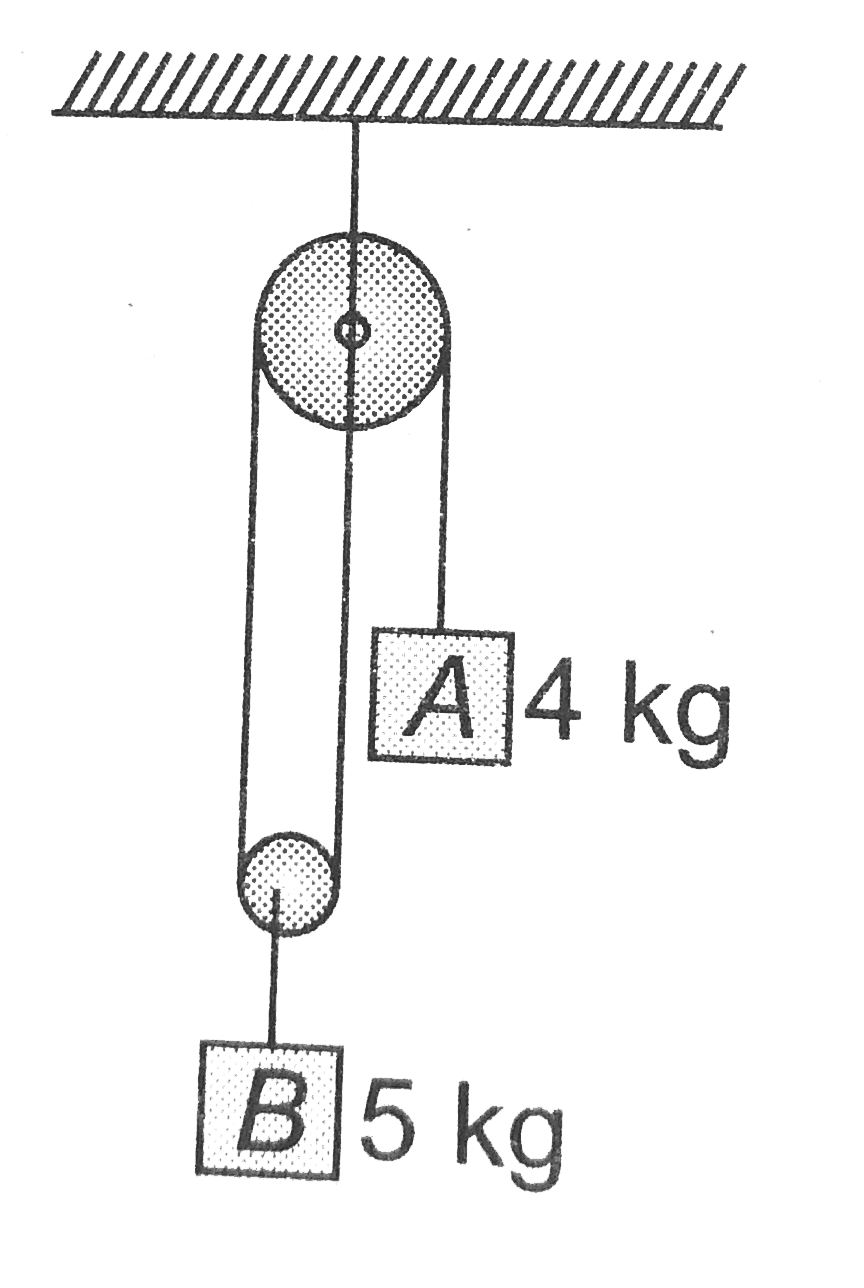
The acceleration of the blocks A and B respectively in situation shown in the figure is : pulleys & strings are mass lessA 2g/7 downward g/7 upwardB2g/3 downward g/3 upwardC10g/13 downward 5g/13 upwardD none of these
Correct Answer is: A 2g/7 downward g/7 upwardaA = 2aB ...1mA g – T = mA aA ...22T – mB g = mB aB ...3Solving we get aA = 2g/7 & aB = g/7
Related Solutions
Find the acceleration of the blocks A and B shown in figure-2.26 (a) and (b) [(a) 10g//13 " forward, "5g//13 " downward, "(b) 8g//13 " downward"]
View SolutionTwo blocks 'A' and 'B' having masses m_(A) and m_(a) , respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?
View SolutionTwo blocks 'A' and 'B' having masses m_(A) and m_(a) , respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?
View SolutionThe acceleration of the block and respectively in situation shown in the figure is: (pulleys and string are massless).
View SolutionIn the figure shown, acceleration of 1 is x (upwards). Acceleration of pulley , w.r.t. pulley is y (downwards) and acceleration of 4 w.r.t. to pulley is z (upwards). Taking upward +ve and downward -ve then
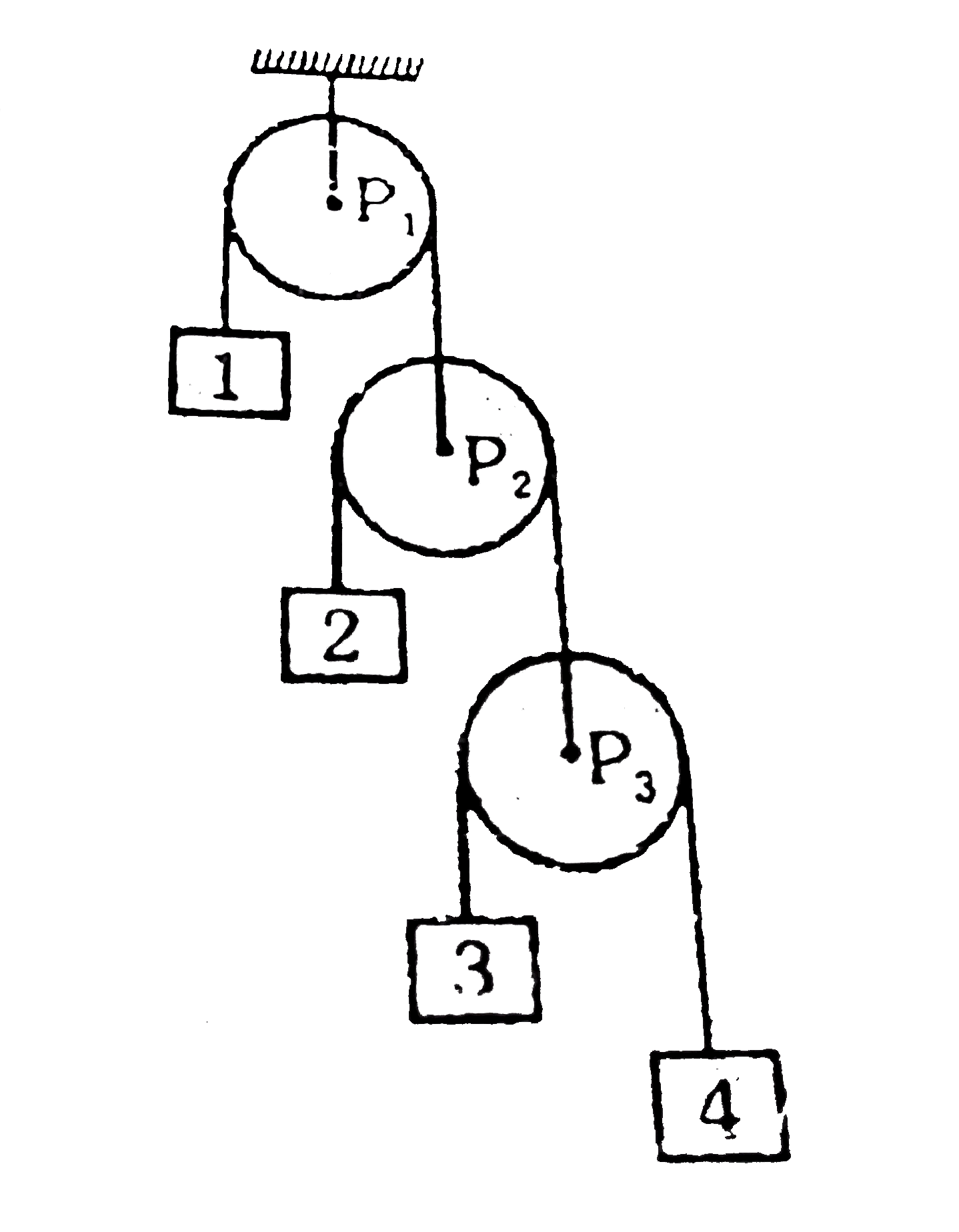
View SolutionIn the figure shown ,acceleration of 1 is x (upwards). Acceleration of pulley with respect to pulley is y (downwards) and acceleration of 4 with respect to pulley is z (upwards). Then match the following

View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are downwards and downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 3.
View SolutionThe pulley system shown in the figure consists of two pulleys of radii 2 m and 1 m respectively. If the acceleration of block A is in the downward direction 5ms^(-2) then the acceleration of block B will be
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are downwards and downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absolute acceleration of block 1.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are downwards and downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absolute acceleration of block 1.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are downwards and downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 2.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1 ms^(-2) downwards and 5ms^(-2) downwards, respectively. Acceleration of block 3 relative to 4 is zero. Find the absoulte acceleration of block 2.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1 ms^(-2) downwards and 5ms^(-2) downwards, respectively. Acceleration of block 3 relative to 4 is zero. Find the absoulte acceleration of block 4.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1 ms^(-2) downwards and 5ms^(-2) downwards, respectively. Acceleration of block 3 relative to 4 is zero. Find the absoulte acceleration of block 4.
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration g/6 to distance x. The work done by the string is
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration (g)/(6) to a distance x. The work done by the string is
View SolutionA body of mass m is allowed to fall with the help of string with downward acceleration (g)/(6) to a distance x. The work done by the string is
View Solution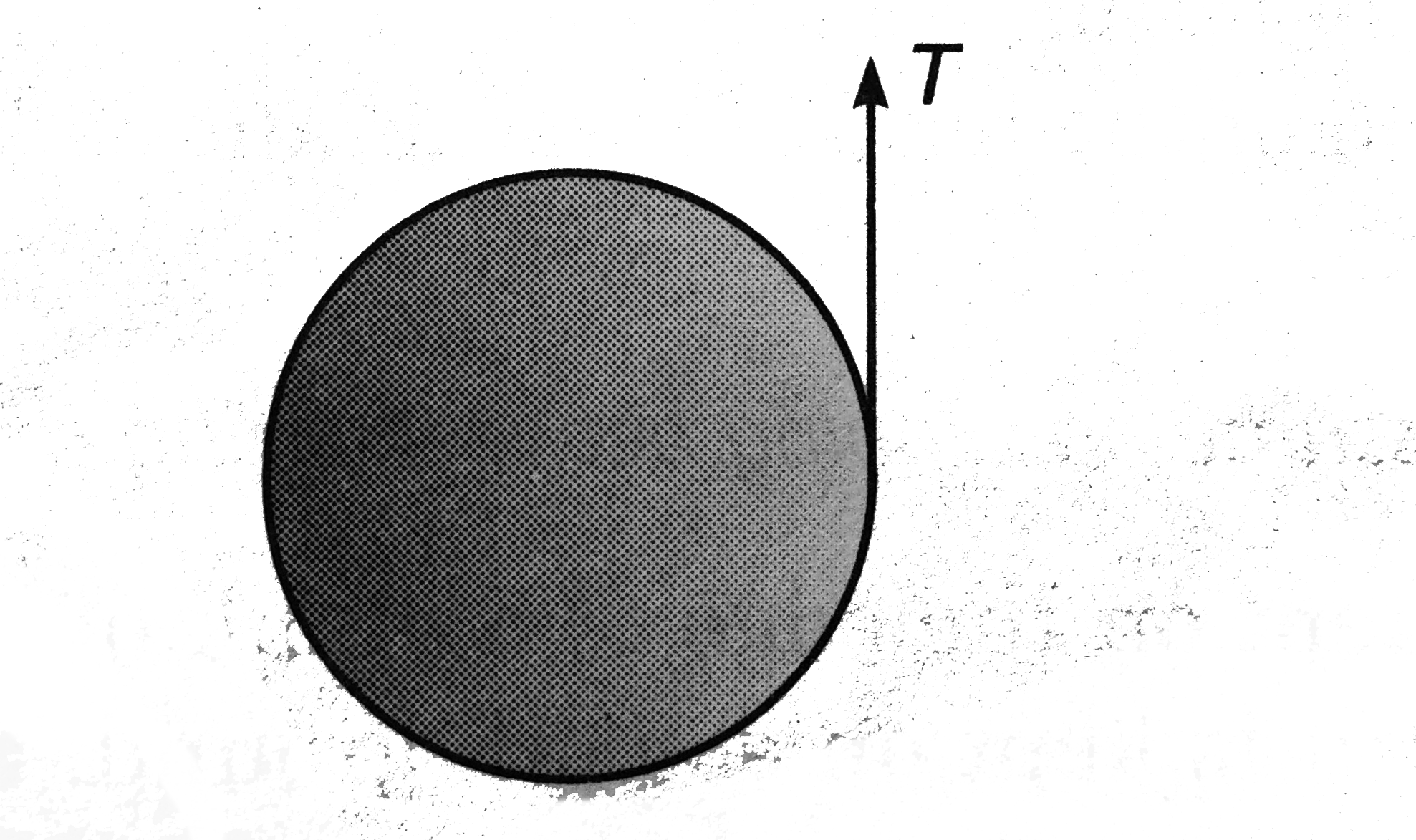
A uniform cylider of mass and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude
(b). Find the tension in the string.
View Solution
A uniform cylider of mass and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude
(b). Find the tension in the string.
View SolutionIn the pulley system shown, if radii of the bigger and smaller pulley are 2 m and 1m respectively and the acceleration of block A is in the downward direction, then the acceleration of block B will be : [Pulleys are fixed to each other]
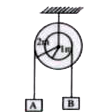
View Solution