A particle moves in a straight line with a velocity given by dx/dt = x + 1 x is the distance described. What is the time taken by a particle to transverse a distance of 99 metres?
We havedx/x + 1 = dtOn integrating we getTherefore time taken by the particle is t = = ln100 loge 102 = 2loge10
Related Solutions
A particle moves in a straight line with a velocity given by (dx)/(dt)=x+1 (x is the distance described). The time taken by the particle to traverse a distance of 99 metres is
View SolutionA partical moves in a straight line with a velocity given by (dx)/(dt)=x+1 (x is the distance described). The time taken by a particle to traverse a distance of 99 metres, is
View SolutionA partical moves in a straight line with a velocity given by (dx)/(dt)=x+1 (x is the distance described). The time taken by a particle to traverse a distance of 99 metres, is
View SolutionA particle moves in a straight line with a velocity given by (x is the distance described).
The time taken by the particle to traverse a distance of 99 metres is
View SolutionA particle moves in a st. line with a velocity given by , (x is the distacne descirbed) . The time taken by a prticle to transverse a distance of 99 metres is :
View Solutionएक कण सरल में वेग (x चली दुरी ) से गति करता है , तो 99 मीटर दुरी तय करने में लिया गया समय है।
View SolutionA particle moves in a line with velocity given by . The time taken by the particle to cover a distance of 9 metre is
View SolutionA particle moves in a line with velocity given by (ds)/(dt)=s+1. The time taken by the particle to cover a distance of 9 metre is (A) 1 (B) log10(C)2log10(D)10
View Solutionएक कण सरल रेखा में गति कर रहा है । t समय पर कण द्वारा चली गई दुरी x निम्न संबंध द्वारा दी जाती है -
समय पर कण का वेग ज्ञात कीजिए ।
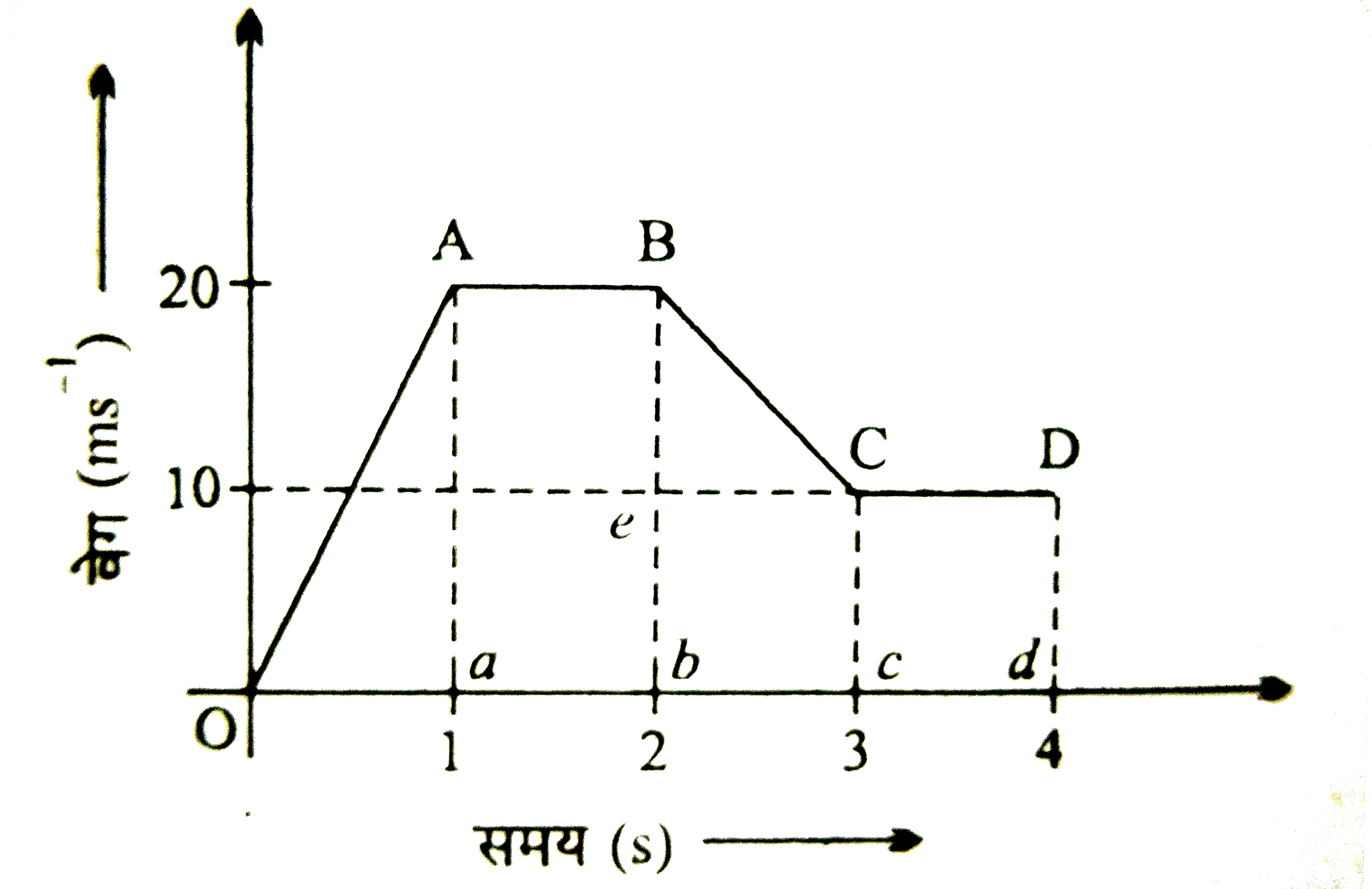
View Solutionसरल रेखा में गतिमान एक कण का वेग समय ग्राफ नीचे दिया गया है। पहले चार सेकंड में कण द्वारा तय दुरी की गणना कीजिए ।
View SolutionParticle is moving in a straight line. Distance x is related to the time t by the equation t=sqrt(x)+3 . Distance x is measured in metres and time t is seconds. After how many seconds will the particle come to the rest?
View SolutionThe distance traversed by a particle moving along a straight lne is given by x = 180t+50t^(2) metre. The acceleration of the particle is
View SolutionThe distance traversed by a particle moving along a straight lne is given by x = 180t+50t^(2) metre. The acceleration of the particle is
View SolutionA particle moves along a straight line OX. What is the distance of the particle from O at a time t (in seconds)? (in metres) x=40+12t-t^(3) is given by. How far will the particle travel before coming to rest?
View SolutionA particle moves along a straight line . At a time (in seconds) the distance (in metre) of the particle is given by . How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line OX. At a time (in second) the distance x (in metre) of the particle from "O' is given by : How long particle travels before coming to rest ?
View SolutionA particle moves along a straight line . At a time (in seconds) the distance (in metre) of the particle is given by . How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line OX . At a time t (in seconds) the distance x (in metre) of the particle is given by x = 40 +12 t - t^3 . How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line OX . At a time t (in seconds) the distance x (in metre) of the particle is given by x = 40 +12 t - t^3 . How long would the particle travel before coming to rest ?
View SolutionThe distance traversed by a particle moving along a straight line is given by x = 180 t + 50 t^(2) metre. Find the velocity at the end of 4s.
View Solution