A particle moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described).
The time taken by the particle to traverse a distance of 99 metres is
log10e
2loge10
2log10e
12log10e
The correct Answer is:B
To solve the problem of finding the time taken by a particle to traverse a distance of 99 meters given the velocity equation dxdt=x+1, we will follow these steps:
Step 1: Separate the Variables
We start with the equation:
dxdt=x+1
We can rearrange this to separate the variables:
dxx+1=dt
Step 2: Integrate Both Sides
Next, we integrate both sides. The left side will be integrated with respect to x and the right side with respect to t:
∫dxx+1=∫dt
The integral of the left side is:
ln|x+1|+C1
And the integral of the right side is:
t+C2
Combining these gives:
ln|x+1|=t+C
where C=C2−C1 is a constant.
Step 3: Solve for the Constant C
To find the constant C, we can use the initial condition. When t=0, we assume the particle starts from x=0:
ln|0+1|=0+C⟹ln(1)=C⟹C=0
Thus, our equation simplifies to:
ln|x+1|=t
Step 4: Solve for Time t when x=99
Now we need to find the time t when the distance x is 99 meters:
ln|99+1|=t⟹ln(100)=t
Step 5: Simplify the Result
Using properties of logarithms, we can express ln(100):
ln(100)=ln(102)=2ln(10)
Thus, the time taken by the particle to traverse 99 meters is:
t=2ln(10)
Final Answer
The time taken by the particle to traverse a distance of 99 meters is:
t=2ln(10)
---
We start with the equation:
dxdt=x+1
We can rearrange this to separate the variables:
dxx+1=dt
Next, we integrate both sides. The left side will be integrated with respect to x and the right side with respect to t:
∫dxx+1=∫dt
The integral of the left side is:
ln|x+1|+C1
And the integral of the right side is:
t+C2
Combining these gives:
ln|x+1|=t+C
where C=C2−C1 is a constant.
To find the constant C, we can use the initial condition. When t=0, we assume the particle starts from x=0:
ln|0+1|=0+C⟹ln(1)=C⟹C=0
Thus, our equation simplifies to:
ln|x+1|=t
Now we need to find the time t when the distance x is 99 meters:
ln|99+1|=t⟹ln(100)=t
Using properties of logarithms, we can express ln(100):
ln(100)=ln(102)=2ln(10)
Thus, the time taken by the particle to traverse 99 meters is:
t=2ln(10)
The time taken by the particle to traverse a distance of 99 meters is:
t=2ln(10)
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBook:ML KHANNAChapter:DIFFERENTIAL EQUATIONSExercise:Problem Set (1) (TRUE AND FALSE)
Explore 8 Videos
- DIFFERENTIAL EQUATIONSBook:ML KHANNAChapter:DIFFERENTIAL EQUATIONSExercise:Problem Set (1) (FILL IN THE BLANKS)
Explore 9 Videos
- DETERMINANTS Book:ML KHANNAChapter:DETERMINANTS Exercise:Self Assessment Test
Explore 19 Videos
- DIFFERENTIATIONBook:ML KHANNAChapter:DIFFERENTIATIONExercise:MESCELLANEOUS EXERCISE
Explore 3 Videos
Similar Questions
A particle moves in a line with velocity given by dsdt=s+1. The time taken by the particle to cover a distance of 9 metre is (A) 1 (B) log10 (C) 2log10 (D) 10
View SolutionA particle moves in a straight line with a velocity which varies as the square of distance from a fixed point .Its acceleration varies as the cube of the distance .
View Solution
Knowledge Check
A partical moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described). The time taken by a particle to traverse a distance of 99 metres, is
Alog10eBloge10C2log10eD12log10e.A particle moves in a straight line with a velocity given by dxdt=x+1 (x is the distance described).
The time taken by the particle to traverse a distance of 99 metres isAlog10eB2loge10C2log10eD12log10eA particle starts from origin with a velocity (in m/s) given by the equation dxdt=x+1. The time (in second) taken by the particle to traverse a distance of 24 m is
Aln 24Bln 5C2 ln 5D2 ln 4
The velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
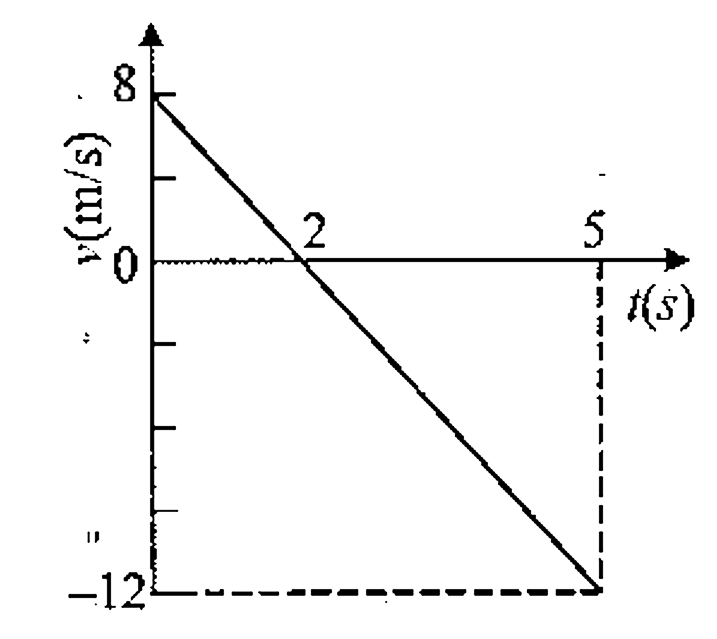
View SolutionA particle moves along a horizontal straight line with a velocity-time relationship as shown in the figure-1.129. The total distance moved by the particle is :
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
View Solution

