The perimeter of a sector is p. The area of the sector is maximum when its radius isA √pB 1/√pC p/2D p/4
Answer is D p/4See Fig. The perimeter of a sector is p. Let AOB be the sector with radius r. If the angle of the sector be θ radians then the area of the sector isA = 1/2r2θ 1Length of the arc iss = rθ or θ = s/rTherefore the perimeter of the sector isp = r + s + r = 2r + s 2Substituting θ = s/r = in Eq. 1 we haveA = 1/2r2s/r = 1/2rs ⇒ s = 2A/rNow substituting the value of s in Eq. 2 we getp = 2r + 2A/r or 2A = pr - 2r2Differentiating w.r.t. r we get2dA/dr = p - 4rWe know that for the maximum value of area isdA/dr = 0 or p - 4r = 0 or r = p/4
Related Solutions
The perimeter of a sector is p , then the area of the sector is maximum when its radius is-
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe perimeter of a sector is p. the area of the sector is maximum when it radius is
View SolutionIf P is the perimeter and r is the radius of a sector, then the area of the sector is maximum, if
View Solutionयदि कोण , त्रिज्या r वाले वृत्त के त्रिज्यखंड का कोण हो, तो त्रिज्यखंड का क्षेत्रफल होगा
View SolutionIn a circle with radius R, the measure of the angle of a sector is . Find the area of that sector.
View SolutionArea of a sector of angle of a circle with radius R is
View SolutionIn the given figure radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm.
Find A (P-ABC)
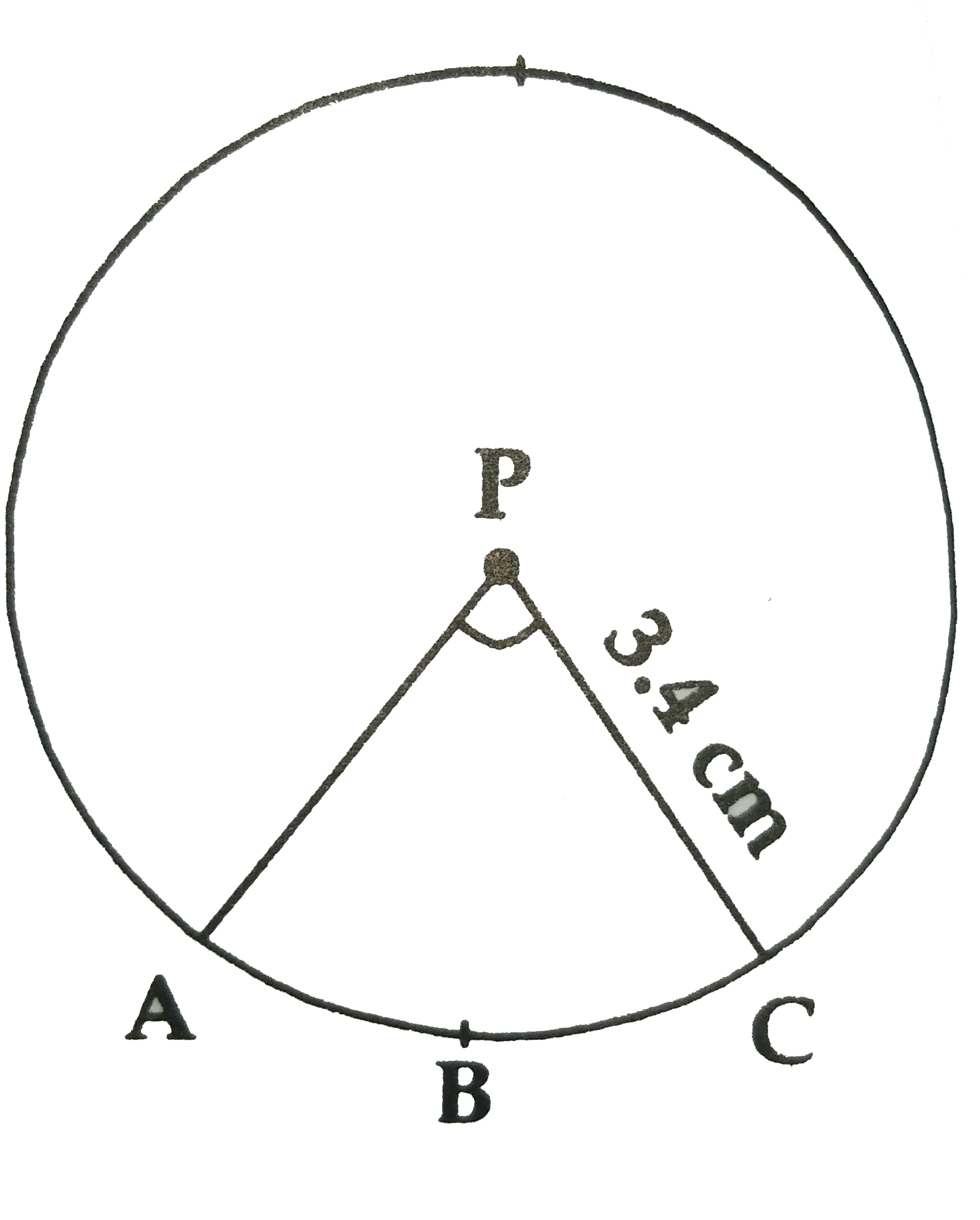
Given: Radius=3.4 cm
P(sector P-ABC)=12.8cm
To find: A(P-ABC)
View SolutionThe perimeter of a sector is given. The area is maximum when the angle of the sector is
View SolutionThe perimeter of a sector is given.The area is maximum when the angle of the sector is
View SolutionIf the perimeter of a sector of a circle is constant then find the angle of the sector, when its area is maximum.
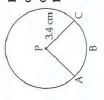
View SolutionIn the adjoining figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm. Find A (P-ABC).
View SolutionIn the adjoining figure, radius of circle is cm and perimeter of sector P-ABC is
cm. Find
A(P-ABC).
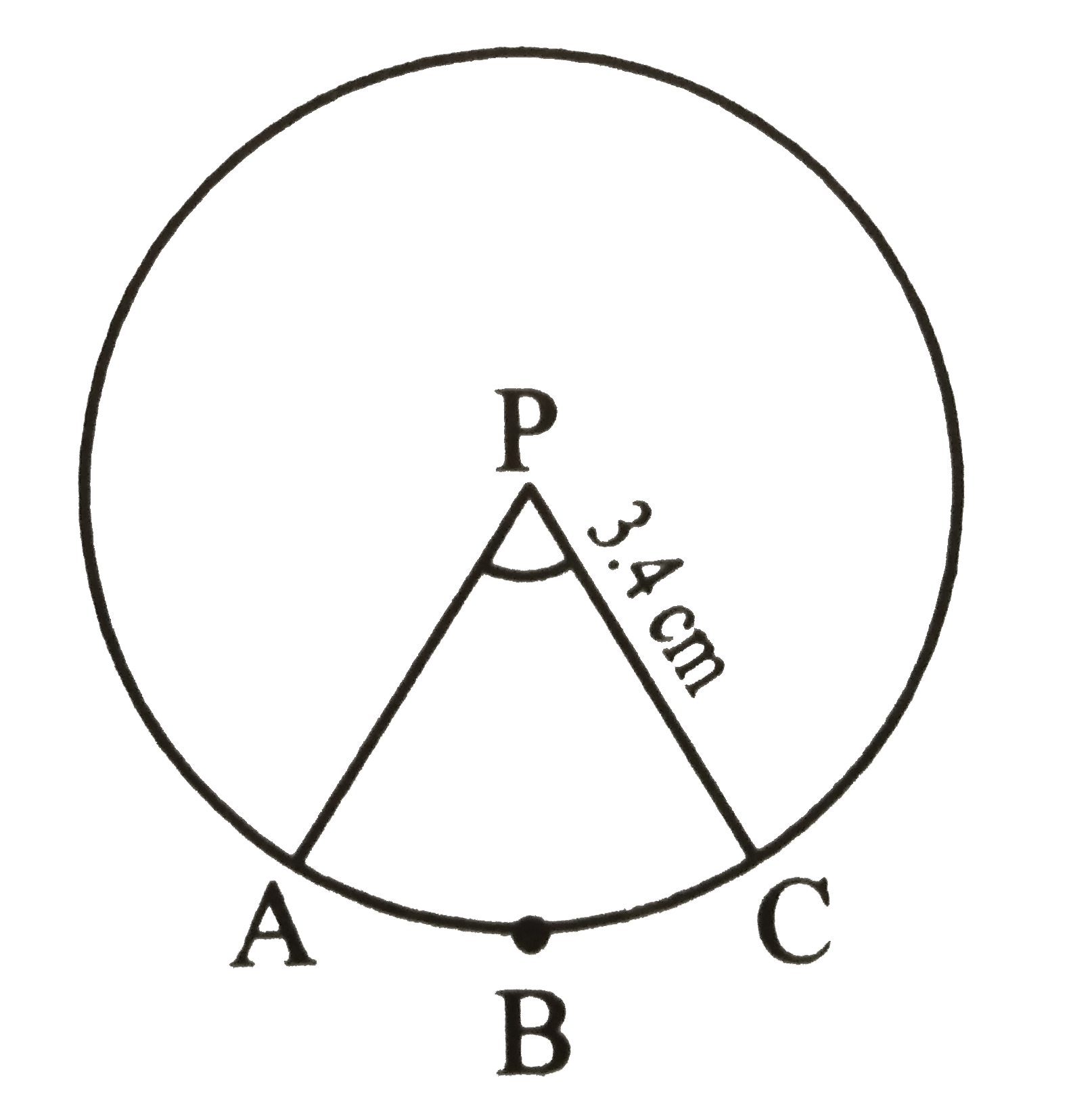
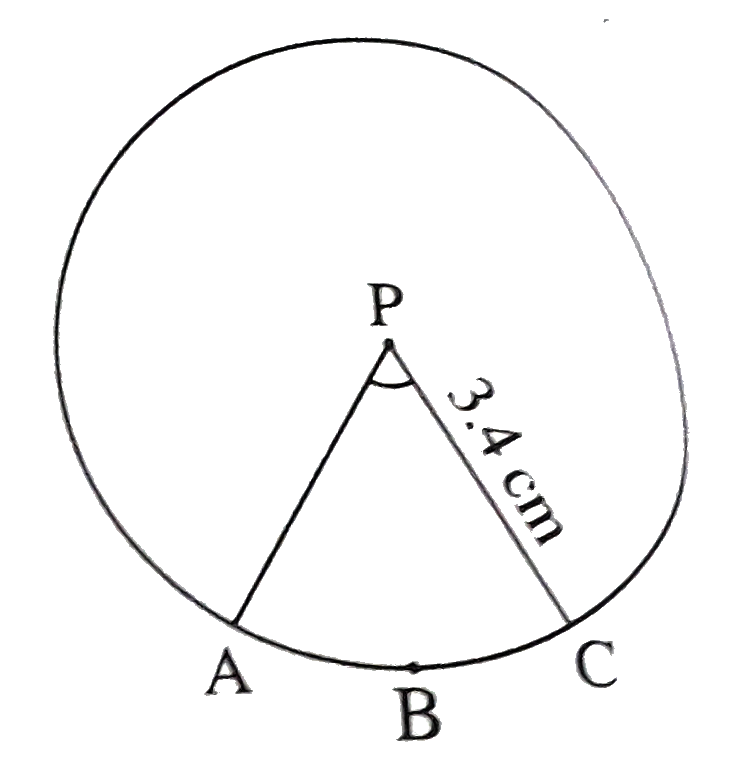
View SolutionIn figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm. Find A(P-ABC).
View SolutionIn the adjoining figure, radius of circle is cm and perimeter of sector P-ABC is
cm. Find
A(P-ABC).
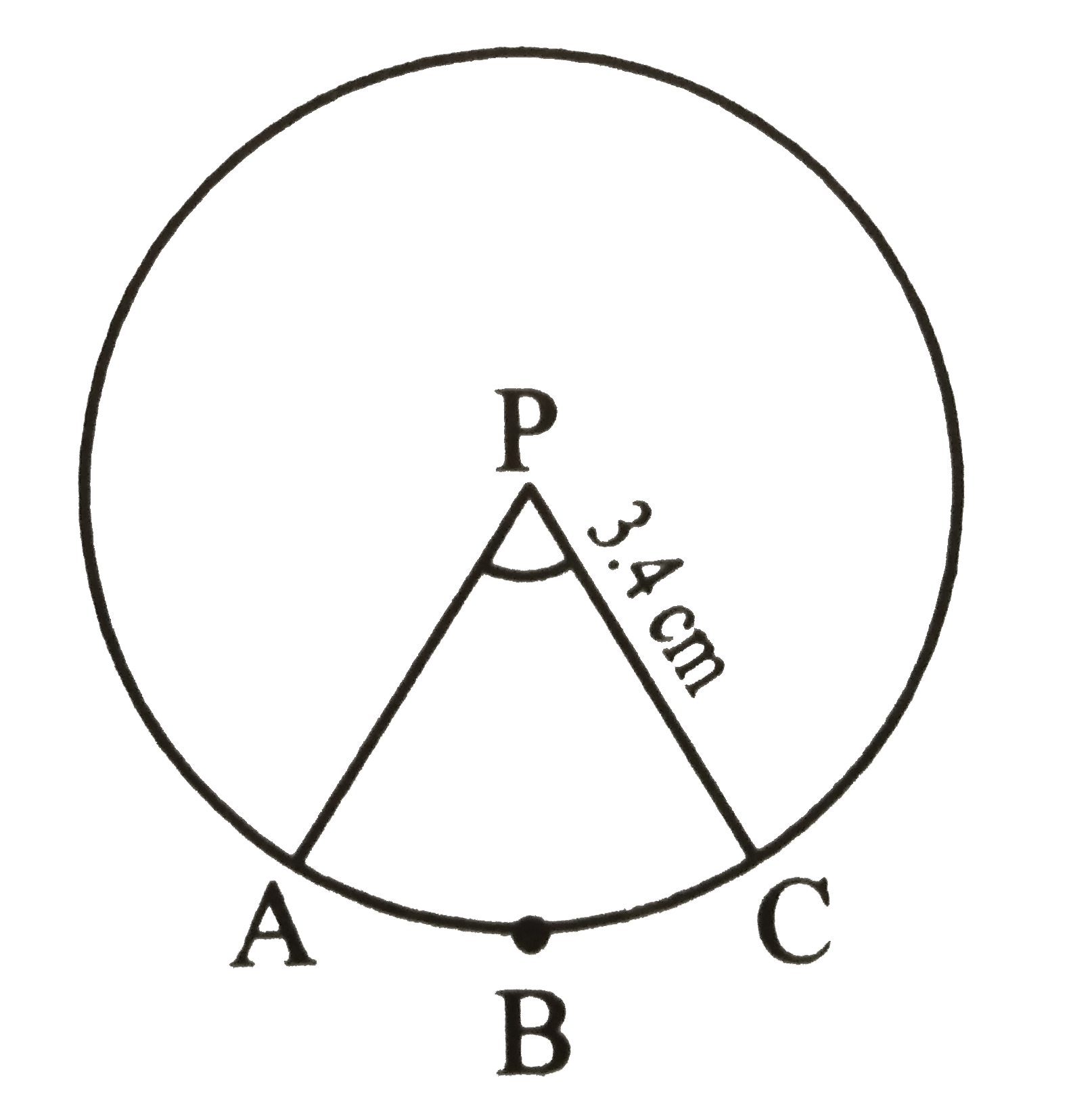
View SolutionThe length of the perimeter of a sector of a circle is 20 cm. Give an expression for the area of the sector in terms of r(the radius of the circle) and hence find the maximum area of the sector.
View Solution