The perimeter of a sector is p. The area of the sector is maximum when its radius is
√p
1√p
p2
p4
The correct Answer is:D
To solve the problem of finding the radius at which the area of a sector is maximized given a fixed perimeter p, we can follow these steps:
Step 1: Understand the Perimeter of the Sector
The perimeter P of a sector of a circle is given by the formula:
P=2r+rθ
where r is the radius and θ is the angle in radians.
Step 2: Express θ in terms of r and p
From the perimeter formula, we can rearrange it to express θ:
p=2r+rθ
This can be rearranged to find θ:
rθ=p−2r⟹θ=p−2rr
Step 3: Write the Area of the Sector
The area A of the sector is given by:
A=12r2θ
Substituting θ from Step 2:
A=12r2(p−2rr)=12r(p−2r)
This simplifies to:
A=p2r−r2
Step 4: Differentiate the Area with respect to r
To find the maximum area, we need to differentiate A with respect to r and set the derivative equal to zero:
dAdr=p2−2r
Setting the derivative to zero for maximization:
p2−2r=0
Step 5: Solve for r
From the equation p2−2r=0, we can solve for r:
2r=p2⟹r=p4
Conclusion
The radius r at which the area of the sector is maximized is:
p4
The perimeter P of a sector of a circle is given by the formula:
P=2r+rθ
where r is the radius and θ is the angle in radians.
From the perimeter formula, we can rearrange it to express θ:
p=2r+rθ
This can be rearranged to find θ:
rθ=p−2r⟹θ=p−2rr
The area A of the sector is given by:
A=12r2θ
Substituting θ from Step 2:
A=12r2(p−2rr)=12r(p−2r)
This simplifies to:
A=p2r−r2
To find the maximum area, we need to differentiate A with respect to r and set the derivative equal to zero:
dAdr=p2−2r
Setting the derivative to zero for maximization:
p2−2r=0
From the equation p2−2r=0, we can solve for r:
2r=p2⟹r=p4
The radius r at which the area of the sector is maximized is:
p4
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Multiple Correct Answer Type10videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type14videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
Similar Questions
What is the area of the sector shown in
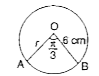 View Solution
View SolutionThe perimeter of a sector is a constant. If its area is to be maximum, the sectorial angle is
View SolutionA wire of length 28 cm is bent to form a circular sector , then the radius (in cm) of the circular sector such that the area of the circular sector is maximum is equal to
View SolutionIf the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is (a) 58 cm2 (b) 52 cm2 (c) 25 cm2 (d) 56 cm2
View SolutionFind the area of the segment of a circle, given that the angle of the sector is 120o and the radius of the circle is 21 cm. (Take π=22/7)
View SolutionIf the pair of lines ax2+2(a+b)xy+by2=0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
View SolutionThe perimeter of a rectangle is 40 cm. Find the dimensions of the rectangle if its area is maximum.
View SolutionThe perimeter of a sector of a circle of radius 5.2cm is 16.4cm. Find the area of the sector.
View SolutionThe radius of a circle is 14 cm and the area of the sector is 102.7cm2. Find the central angle of the sector.
View SolutionIf the perimeter of a triangle is 6, then its maximum area is
View Solution
