A satellite can be in a geostationary orbit around a planet at a distance r from the centre of the planet. If the angular velocity of the planet about its axis doubles a satellite can now be in a geostationary orbit around the planet if its distance from the centre of the planet is.a r/2 b r/2√2 c r/41/3 d r/21/3
Correct Answer is: c r/41/3 Time period of rotation T and distance r are related as T2 ∝ r3. Also when the angular velocity doubles the time period becomes half.
Related Solutions
A satellite can be in a geostationary orbit around a planet at a distance r from the centre of the planet . If the angular velocity of the planet about its axis doubles, a satellite can saw be in a geostationary orbit around the planet if its distance from the centre of the planet is
View SolutionA satellite can be in a geostationary orbit around earth at a distance r from the centrer. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit around if its distance from the centre is
View SolutionIf the angular velocity of a planet about its own axis is halved, the distance of geostationary satellite of this planet from the centre of the centre of the planet will become
View SolutionIf the angular velocity of a planet about its own axis is halved, the distance of geostationary satellite of this planet from the centre of the centre of the planet will become
View SolutionIf the velocity of a planet relative to its axis is halved, then the distance of the geostationary satellite of this planet from the center of the planet will be
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius . If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius r . If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius . If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
View Solutionएक ग्रह सूर्य के चारों ओर किसी दीर्घवृत्तीय कक्षा में परिक्रमण कर रहा है। इसकी सूर्य से निकटतम दूरी r है तथा दूरस्थ दूरी R है। यदि सूर्य से निकटतम ग्रह का वेग v हो तथा सूर्य से दूरस्थ ग्रह का वेग V हो, तो v/V= ?
View SolutionIf a satellite is revolving around a planet of mass Min an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance are from the planet will be given by
View SolutionA satellite is in a circular orbit around a planet . Its period of revolution is T, radius of the orbit is R, orbital velocity V and acceleration .a. , then
View SolutionA satellite is in a circular orbit around a planet. Its period of revolution is T, radius of the orbit is R, orbital velocity V and acceleration 'a', then
View SolutionA satellite is in a circular orbit around a planet. Its period of revolution is T, radius of the orbit is R, orbital velocity V and acceleration 'a', then
View SolutionA satellite is in a circular orbit around a planet . Its period of revolution is T, radius of the orbit is R, orbital velocity V and acceleration .a. , then
View SolutionConsider a hypothetical planet which is very long and cylinderical. The density of the planet is , its radius is .
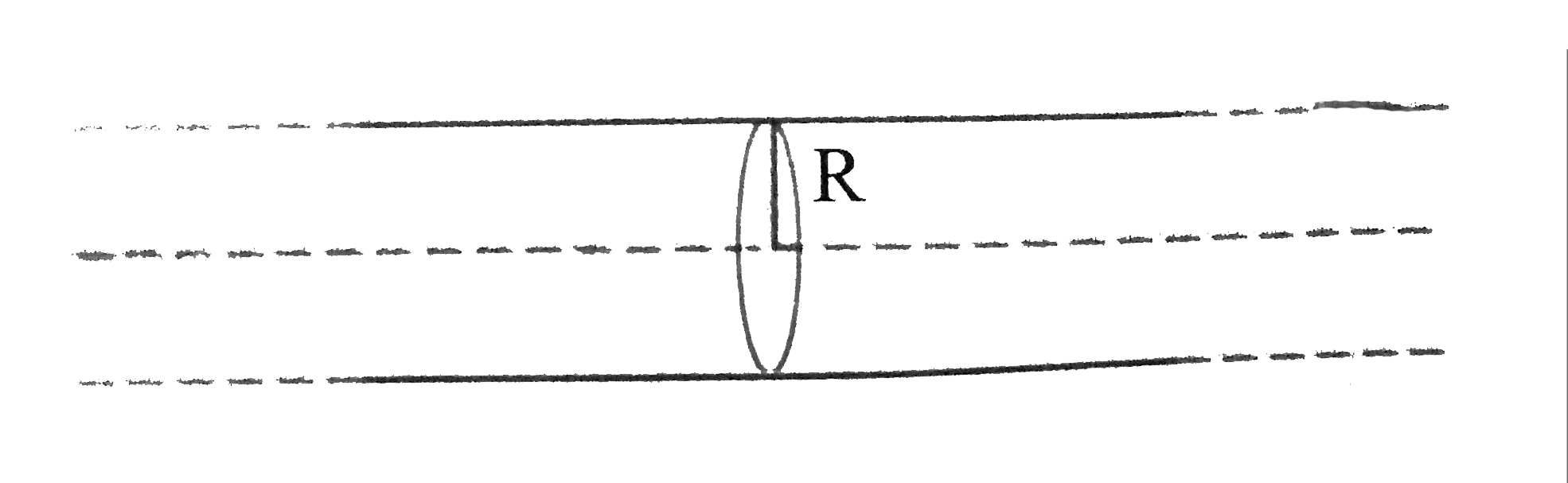
What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?
View SolutionConsider a hypothetical planet which is very long and cylinderical. The density of the planet is rho , its radius is R . What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?
View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius r. IF the angular velocity of earth about its axis doubles, a satellites can now be in a geostationary orbit around earth of radius is (r )/((x)^(1//3)) . Find the value of x
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R . If the orbital velocity of the planet closest to the Sun is v , then what is the velocity at the farthest point?
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R . If the orbital velocity of the planet closest to the Sun is v , then what is the velocity at the farthest point?
View SolutionA planet orbits the Sun in time T at a distance of R from it. Another planet orbits the Sun in a time of 8T. What is its distance R' from the Sun.
View Solution