When a capacitor discharges through a resistance R the time constant is τ and the maximum current in the circuit is i0.a The initial charge on the capacitor was i0τ.b The initial charge on the capacitor was 1/2 i0τc The initial energy stored in the capacitor was i02Rτ.d The initial energy stored in the capacitor was 1/2 i02Rτ.
Related Solutions
A charged capacitor is connected to an inductor . At a particular instant, energy stored in inductor is 8/9 times of initial energy stored In capacitor . What is the ratio of initial charge on capacitor to that with instantaneous charge on capacitor ?
View SolutionIf the charge on capacitor is increased by 5C, the energy stored in the capacitor is increased by 21%, what will be initial charge on the capacitor ?
View SolutionWhen a charged capacitor is discharged through a resistor, heat is produced in the resistor
In charging a capacitor, energy is stored in the capacitor.
View SolutionA fully charged parallel plate capacitor is connected across an unchanged identical capacitor . Show that the energy stored in the combination is less than that stored initially in the single capacitor .
View SolutionThe capacitor of capacitance C in the circuit shown in fully charged initially. Resistance is R.– After the switch S is closed, the time taken to reduce the stored energy in the capacitor to half its initial value is
View SolutionA charged 30muF capacitor is connected to a 27mH inductor. If the initial charge on the capacitor is 6mC then What is the total energy stored in the circuit initially. What is the total energy at a later time?
View SolutionA charged 30 micro Farad capacitor is connected to a 20 mH inductor. Suppose the initial charge on the capacitor is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionIn the circuit shown in fig. find the maximum energy stored on the capacitor. Initially, the capacitor was uncharged.
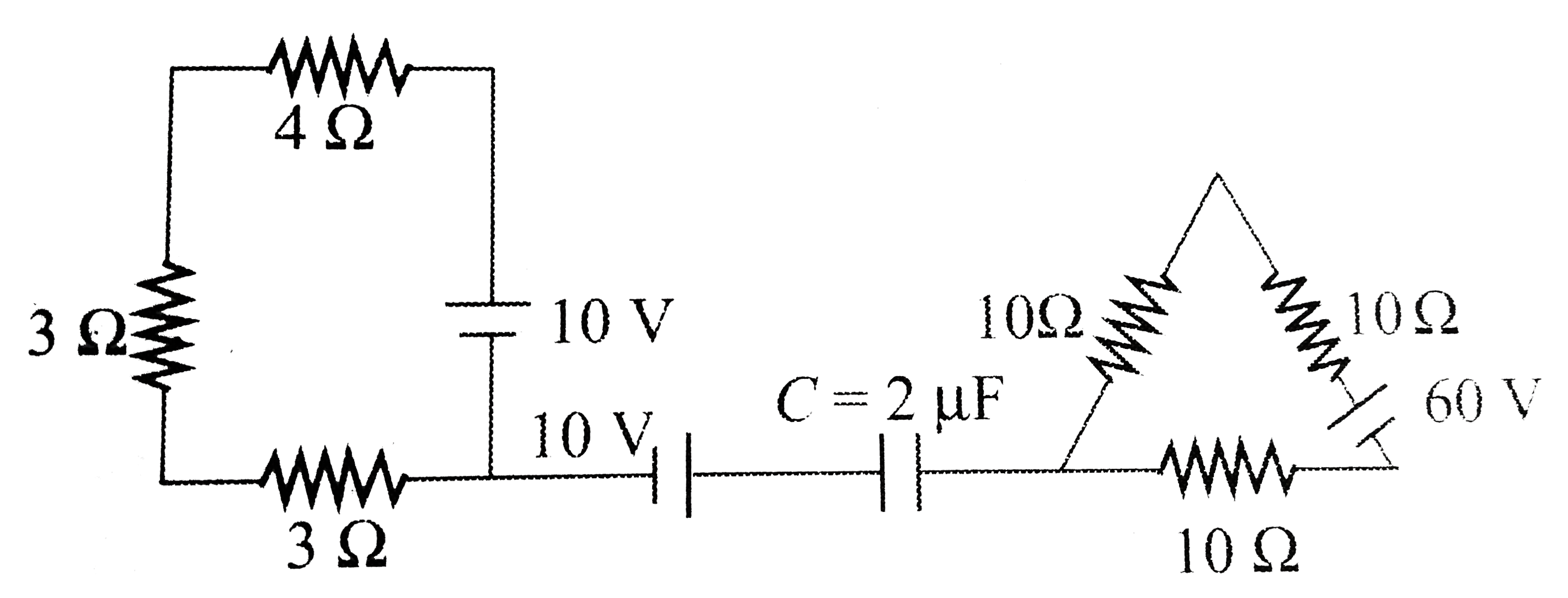
View SolutionIn the circuit shown in fig. find the maximum energy stored on the capacitor. Initially, the capacitor was uncharged.
View SolutionSuppose the initial charge on the capacitor in Exercise 7.7 is 6 mC. What is the total energy stored in the circuit initially ? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor given in above question is 6 mC.What is the total energy stored in the circuit initially ? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in Exercise 7.7 is 6mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in Exercise 7.7 is 6 mC. What is the total energy stored in the circuit initially ? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor in is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionSuppose the initial charge on the capacitor is 6 mC. What is the total energy stored in the circuit initially? What is the total energy at later time?
View SolutionInitially capacitor is uncharged at t = 0 switch is closed. Charge on capacitor when current in the circuit is 10 % of maximum current :
View SolutionInitially capacitor is uncharged at t = 0 switch is closed. Charge on capacitor when current in the circuit is 10 % of maximum current :
View Solution