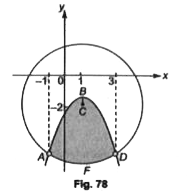
Find the area enclosed between the smaller arc of the circle x2 + y2 – 2x + 4y – 11 = 0 and the parabola y = – x2 + 2x + 1 – 2√3.
Given curves are x2 + y2 – 2x + 4y – 11 = 0 and y = –x2 + 2x + 1 – 2√3 x – 12 + y + 22 = 16 and y + 2√3 – 1 = – x – 12 Hence the required area
Related Solutions
Find the equation of the radical axis of the following circles. is
View Solution. Find current enclosed in the loopMagnetic field at a point (x, y, z) is given by B- Boyix2 + y = 2(x2 + y2)2__Box(x2 + y2)2
View Solution2.10 The radii of the circles x2 + y2 = 1, x2 + y2 – 2x – 6y = 6 and x2 + y2 - 4x - 12y = 9 are in(A)AP.(B)GP.(C) H.P.(D) None
View SolutionFind the areas enclosed between the circle and the parabola
View SolutionFind the third proportional to and (x+y)
View SolutionFind the derivate of : y = sin^(–1) (2x √(1−x2))
View SolutionFind the area enclosed between parabola
and the straight line 2x - y + 3 = 0
View SolutionIf(x2+y2)=aetan(y/x),a>0 then y(0) is (A)#220-1/2 ach?D Does not exist
View SolutionFind the equations of all lines having slope 0 which are tangent to the curve
View Solution3.(1) x + y = 0(2) x - y = 0If tangents are drawn from the origin to the curve y = sin x, then their points of contact lie on the curve(3) x2 - y2 = x2y2 (4) x2 + y2 = x2y2(2) x + y = xy(1) X- y = xy
View SolutionFind the polar of the point (−2,3) with respect to the circle x2+y2−4x−6y+5=0
View SolutionFind the smaller of the area bounded by the parabola and the ellipse
View SolutionThe area enclosed between the parabola and lines is…….
View SolutionThe area enclosed between the parabola and line y=2x is
View SolutionFind the value of ∫2x cos (x2 – 5).
View SolutionFind the smaller of the two areas enclosed by the curves .
View SolutionFind the smaller of the two areas enclosed by the curves and .
View SolutionSolve the equation for
View SolutionFind the area enclosed between the parabola and the line .
View SolutionFind the area enclosed by the parabola and the line .
View Solution