Evaluatex →0 px - qx/rx - sx.
Applying L’Hospital’s rule we have
Related Solutions
If is a factor of then show that p+r+t=q+s=0.
View Solutionif lim_(x rarr0)(sqrt(px^(2)+qx)-rx)=2 then
View SolutionIf is a R.E. of second type then
View Solutionतीन रेखाएँ px +qy+r = 0,qx +ry+p = 0, rx + py+q=0 संगामी होगी, यदि
View SolutionThe lines are concurrant then
View SolutionThree lines px + qy + r = 0, qx + ry + p = 0 and rx + py + q = 0 will be concurrent, if -
View SolutionThe lines px +qy+r=0, qx + ry + p =0,rx + py+q=0, are concurrant then
View SolutionThe lines px+qy+r=0,qx+ry+p=0,rx+py+q=0 are concurrant then
View SolutionThe lines are concurrant then
View SolutionThree lines , and are concurrent , if
View Solutionतीन रेखाओं संगामी है, यदि-
View SolutionThree lines px + qy+r=0, qx + ry+ p = 0 and rx + py + q = 0 are concurrent of
View Solutionतीन रेखाएँ और संगामी होंगी, यदि
View Solutionगुणनखण्ड निकालें:
px+qx+rx-py-qy-ry
View SolutionIf the equations px^(2)+qx+r=0 and rx^(2)+qx+p=0 have a negative common root then the value of (p-q+r)=
View SolutionIf then prove that the roots of the equations are in H.P.
View SolutionIf then prove that the roots of the equations are in Н.Р.
View Solutionयदि , तब
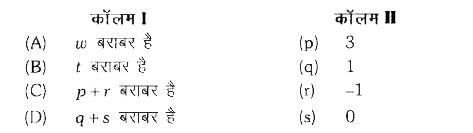
View SolutionIf px^(4)+qx^(3)+rx^(2)+sx+t=|{:(x^(2)+3x,x-1,x+3),(x^(2)+1,2-x,x-3),(x^(2)-3,x+4,3x):}| then t is equal to
View SolutionIf px^(4)+qx^(3)+rx^(2)+sx+t=|{:(x^(2)+3x,x-1,x+3),(x^(2)+1,2-x,x-3),(x^(2)-3,x+4,3x):}| then t is equal to
View Solution