A company produces soft drinks that has a contract which requires that a minimum of 80 units of the chemical A and 60 units of the chemical B go into each bottle of the drink. The chemicals are available in prepared mix packets from two different suppliers. Supplier S had a packet of mix of 4 units of A and 2 units of B that costs Rs.10. The supplier T has a packet of mix of 1 unit of A and 1 unit of B costs Rs.4. How many packets of mixed from S and T should the company purchase to honour the contract requirement and yet minimize cost? Make a LPP and solve graphically
Let x and y units of packet of mixes are purchased from S and T respectively. If z is total cost thenz = 10x + 4y ...iisobjective function which we have to minimizeHere constraints are.On plotting graph of above constraints or inequalities ii iii iv and v we get shaded region having corner point A P B as feasible region.For coordinate of PPoint of intersection of2x + y = 60 ...viand 4x + y = 80 ...viivi – vii => 2x + y - 4x - y = 60 - 80=> -2x = -20 Þ x = 10=>y = 40co-ordinate of P ≡10 40Now the value of z is evaluated at corner point in the following tableSince feasible region is unbounded. Therefore we have to draw the graph of the inequality.10x + 4y < 260 ...viiiSince the graph of inequality viii does not have any point common.So the minimum value of z is 260 at 10 40.i.e. minimum cost of each bottle is Rs.260 if the company purchases 10 packets of mixes from S and 40 packets of mixes from supplier T.
Related Solutions
A company produces soft drinks that has a contract which requires that a minimum of 80 units of the chemical A and 60 units of the chemical B go into each bottle of the drink. The chemicals are available in prepared mix packets from two different suppliers. Supplier S had a packet of mix of 4 units of A and 2 units of B that costs Rs.10. The supplier T has a packet of mix of 1 unit of A and 1 unit of B costs Rs.4. How many packets of mixed from S and T should the company purchase to honour the contract requirement and yet minimize cost? Make a LPP and solve graphically.
View SolutionA company produces soft drinks that has a contract which requires that a minimum of 80 units of the chemical A and 60 units of the chemical B to go into each bottle of the drink. The chemicals are available in a prepared mix from two different suppliers. Supplier S has a mix of 4 units of A and 2 units of B that costs Rs. 10, the supplier T has a mix of 1 unit of A and 1 unit of B that costs Rs. 4. How many mixes from S and T should the company purchase to honour contract requirement and yet minimize cost?
View SolutionA company producing soft drinks has a contract which requires a minimum of 80 units of chemical A and 60 units of chemical B to go in each bottle of the drink. The chemicals are available in a prepared mix from two different suppliers.Suppleer X has a mix of 4 units of A and 2 units of B that costs Rs.10, and the supplier Y has a mix of 1 unit of A and 1 unit of B that costs Rs4. How many mixes from X and Y should the company purchase to honour the contract requirement and yet minimize the cost ?
View SolutionA factory produced two types of chemicals A and B. The following table gives the units of ingredients P and Q (per kg) of chemicals A and B as well as minimum requirements of P and Q and also cost per kg. chemicals A and B :

Find the number of units of chemicals A and B should be produced sp as to minimize the cost.
View SolutionA factory produced two types of chemicals A and B The following table gives the units of ingredients P & Q (per kg) of Chemicals A and B as well as minimum requirements of P and Q and also cost per kg. of chemicals A and B.
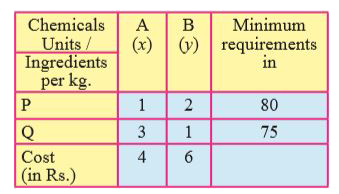
Find the number of units of chemicals A and B should be produced so as to minimize cost.
View SolutionA company manufactures two types of chemicals A and B. Each chemical requires the types of raw materials P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.

The company gets profit of Rs. 350 and RS.400 by selling one unit of A and one unit of B respectively. If the entire production of A and B is sold, then formulate the problem as LPP.
View SolutionA farmer mixes two brands and of cattle feed. Brand costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand costing Rs. 200 per bag contains 1.5 units of nutritonal element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A,B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs. 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag ?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A,B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionA farmer mixes two brands and of cattle feed. Brand costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand costing Rs. 200 per bag contains 1.5 units of nutritonal element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A,B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag, contains 1.5 units of nutritional element A, 1.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and Care 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
View Solutionएक किसान को अपनी खेती के लिए रासायनिक A,B और C के कम-से-कम 10, 12 और 12 इकाइयों की आवश्यकता होती है एक द्रव खाद में प्रति जार A,B,C के क्रमशः 5,2 और 1 इकाइयाँ है जबकि एक सूखे खाद में A,B,C की क्रमशः 1,2 और 4 इकाइयाँ प्रति पैकेट है यदि द्रव खाद 30 रू प्रति जार एवं सूखा खाद 20 रू प्रति पैकेट बिकता हो, किसान को कितने जार और कितने पैकेट खरीदना चाहिए ताकि आवश्यकता की पूर्ती करते हुए खर्च न्यूनतम हो ।
View Solutionएक बीमार व्यक्ति के लिए एक आहार से कम-से-कम विटामिन की इकाइयां , खनिज की इकाइयां और कैलोरीज की इकाइयां होनी चाहिए दो भोज्य और उपलब्ध है जिनकी कीमत क्रमशः रू और रू प्रति इकाई है यदि की एक इकाई में विटामिन की इकाई खनिज की इकाई और कैलोरीज की इकाई हो एवं की एक इकाई में विटामिन की इकाई खनिज की इकाई और कैलोरीज की इकाई हो तो ज्ञात करें की भोज्यों का कैसा सम्मिश्र किया जाए की आवश्यक तत्वों को पूरा करते हुए मूल्य न्यूनतम हो ?
View Solutionएक महिला दो प्रकार के भोज्यों को इस प्रकार मिलाना चाहती है की मिश्रण में विटामिन A कम-से-कम 8 मात्रक और विटामिन B कम-से-कम 11 मात्रक हो । प्रथम भोज्य की लागत Rs 60 प्रति किग्रा और दूसरे भोज्य की लागत Rs 80 प्रति किग्रा है । प्रथम प्रकार के भोज्य के एक किग्रा में 3 मात्रक विटामिन A और 5 मात्रक विटामिन B है जबकि दूसरे प्रकार के भोज्य के एक किग्रा में 4 मात्रक विटामिन A और 2 मात्रक विटामिन B है । मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs. 200 pre bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element c. The minimum requirements of nutrients A,B and C are 18 units, and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag.
View SolutionA farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs. 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs. 200 pre bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element c. The minimum requirements of nutrients A,B and C are 18 units, and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag.
View SolutionA chemical company produces a chemical containing three basic elements A, B, C so that it has at least 16 liters of A, 24 liters of B and 18 liters of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 liters of A, 12 liters of B, 2 liters of C. Each unit of compound II has 2 liters of A, 2 liters of B and 6 liters of C. The cost per unit of compound I is Rs.800/- and that of compound II is Rs.640/-. Formulate the problem as L.P.P. and solve it to minimize the cost.
View SolutionA Chemical company produces a chemical containing three basic elements A, B, C so that it has at least 16 liters of A, 24 liters of B and 18 liters of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 liters of A, 12 liters of B, 2 liters of C Each unit of compound II has 2 liters of A, 2 liters of B and 6 liters of C. The cost per unit of compound I is Rs. 800 and that of compound II is Rs. 640 Formulate the problem as LPP. and solve it to minimize the cost.
View SolutionA company is making two products A and B. The cost of producing one unit of products A and B are Rs. 60 and 80 respectively. As per the agreement, the company has to supply at least 200 units of product B to its regular customers. One unit of product A requires one machine hour whereas product B has machine hours available abundantly within the company. Total machine hours available for product A are 400 hours. One unit of each product A and B requires one labour hour each and total of 500 labour hours are available. The company wants to minimize the cost of production by satisfying the given requirements. Formulate this problem as a LPP.
View Solution