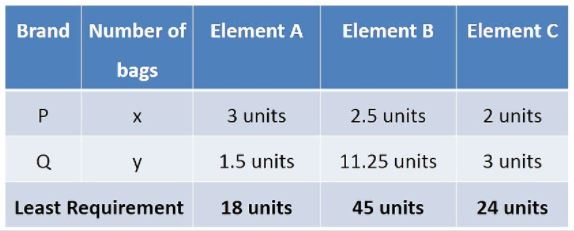
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?

Video Solution

Text Solution

Verified by Experts

Let the mixture contain
$x$ bags of brand P & $y$ bags of brand Q

According to Question:

Element A
Brand P $\to$ 3 units
Brand Q $\to$ 15 units
Least Requirement $\to$ 18 units
$∴$
$3 x + 1.5 y \geq 18$
$2 x + y \geq 12$

Element B
Brand P $\to$ 2.5 units
Brand Q $\to$ 11.25 units
Least Requirement $\to$ 45 units
$∴$
$2.5 x + 11.25 y \geq 45$
$2 x + 9 y \geq 36$

Element C
Brand P $\to$ 2 units
Brand Q $\to$ 3 units
Least Requirement $\to$ 24 units
$∴$
$2 x + 3 y \geq 24$

Also. $x, y \geq 0$

We need to Minimize the cost, hence the function used here is Minimum $Z$ .

Now,
Cost of brand P $\to$ Rs 250
Cost of brand Q $\to$ Rs 200

$∴$ Minimize $Z = 250 x + 200 y$

Combining all constraints
Min $Z = 250 x + 200 y$

Subject to constraints
$2 x + y \geq 12$
$2 x + 9 y \geq 36$
$2 x + 3 y \geq 24$
$x \geq 0, y \geq 0$

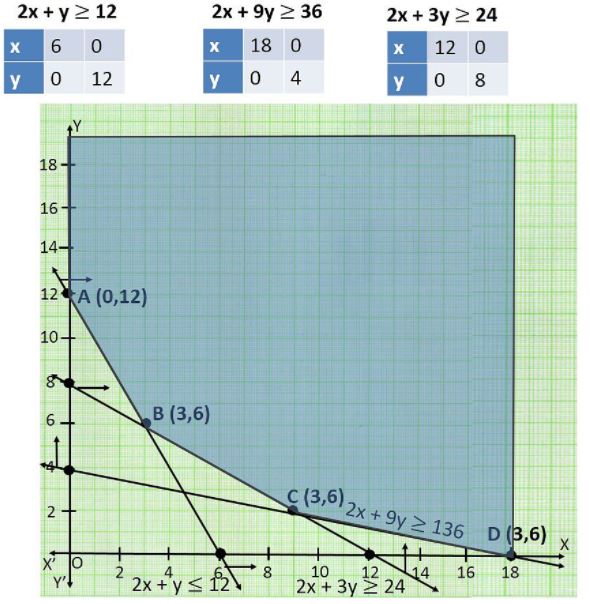
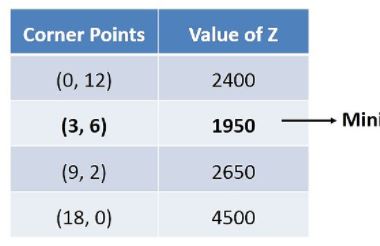
As the feasible region is unbounded, hence, 1950 may or may not be the minimum value of $Z$

For this we need graph inequality
$250 x + 200 y < 1950$

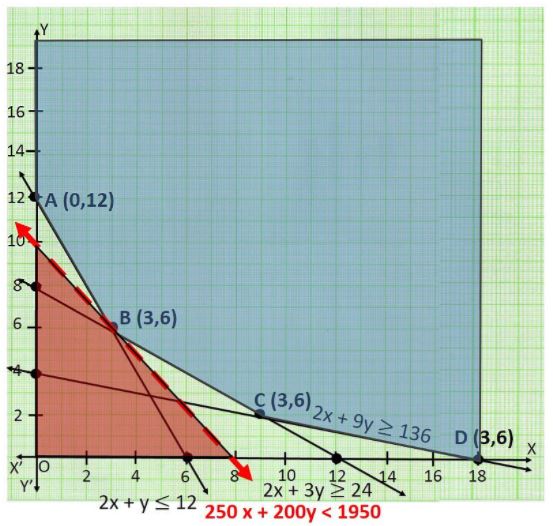
Since there is no common point between the feasible region of the inequality.

Hence, the cost will be minimum if

The mixture contains = 3 bags of brand P
and
The mixture contains = 6 bags of brand Q

Updated on:21/07/2023