Let Ap2 – p Bq2 – q Cr2 – r be the vertices of a triangle ABC. A parallelogram AFDE is drawn with vertices D E and F on the line segments BC CA and AB respectively. Using calculus show that the maximum area of such a parallelogram is 1/4p + q p + rq + r.
Let AF = x = DE and AE = y = DF and AB = c BC = a and CA = b respectively.Since the triangles CAB and CED are similar so CE/CA = DE/AB⇒ b – y/b = x/cNow area of the parallelogram AFDE = P = AF.EM = xy sinA⇒ P = xy sinA⇒ p = x .b1 – x/csinA⇒ dP/dx = b/cc – 2xsinAFor extremum dP/dx = 0
Related Solutions
Let be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is
View SolutionLet be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is .
View SolutionLet be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is
View SolutionLet be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is .
View SolutionLet be the vertices of triangle ABC. A parallelogram AFDE is drawn with D,E, and F on the line segments BC, CA and AB, respectively. Using calculus, show that the maximum area of such a parallelogram is .
View SolutionLet be the vertices of the . A parallelogram is drawn with vertices D, E and F on the line segments BC, CA and AB respectively Find the maximum area of parallelogram .
View Solutionमाना त्रिभुज ABC के शीर्ष है। रेखा खण्ड BC, CA तथा AB पर क्रमशः बिन्दु D, E तथा Fको शीर्ष लेकर एक समान्तर चतुर्भुजAFDE बनाया जाता है। अवकलन का उपयोग करके प्रदर्शित कीजिए कि समान्तर चतुर्भुज का अधिकतम क्षेत्रफल होगा।
View SolutionP,Q,R are the points on the sides AB, BC and CA respectively of triangle ABC such that AP:PB=BQ:QC=AR:RC=1:2. Show that PBQR is a parallelogram.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a . Show that:- BDEF is a parallelogram.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
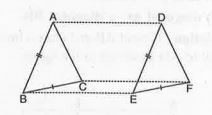 Show that quadrilateral ABED is a parallelogram.
Show that quadrilateral ABED is a parallelogram.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral ABED is a parallelogram.
Show that quadrilateral ABED is a parallelogram.
View SolutionP,Q,R are the points on the sides AB, BC and CA respectivelyh of AP:PB=BQ:Qc=AR:RC=1:2. Show that POBQR is a parallelogram
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
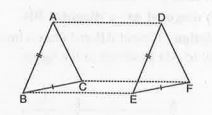 Show that quadrilateral ACFD is a parallelogram.
Show that quadrilateral ACFD is a parallelogram.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral ACFD is a parallelogram.
Show that quadrilateral ACFD is a parallelogram.
View SolutionIn a , if p,q,r are the distances from the orthocentre to the vertices A,B,C respectively, then a q r + b r p+ c p q =
View SolutionStatement 1: ABC is given triangle having respective sides a,b,c. D,E,F are points of the sides BC,CA,AB respectively so that AFDE is a parallelogram. The maximum area of the parallelogram is 1/4 bcsinA. Statement 2 : Maximum value of 2kx--x^2 is at x = k.
View SolutionStatement 1: ABC is given triangle having respective sides a,b,c. D,E,F are points of the sides BC,CA,AB respectively so that AFDE is a parallelogram. The maximum area of the parallelogram is 1/4 bcsinA. Statement 2 : Maximum value of is at x = k.
View SolutionShow that the points (p , q , r) , (q , r , p) and (r , p , q) are the vertices of an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that BDEF is a parallelogram
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View Solution