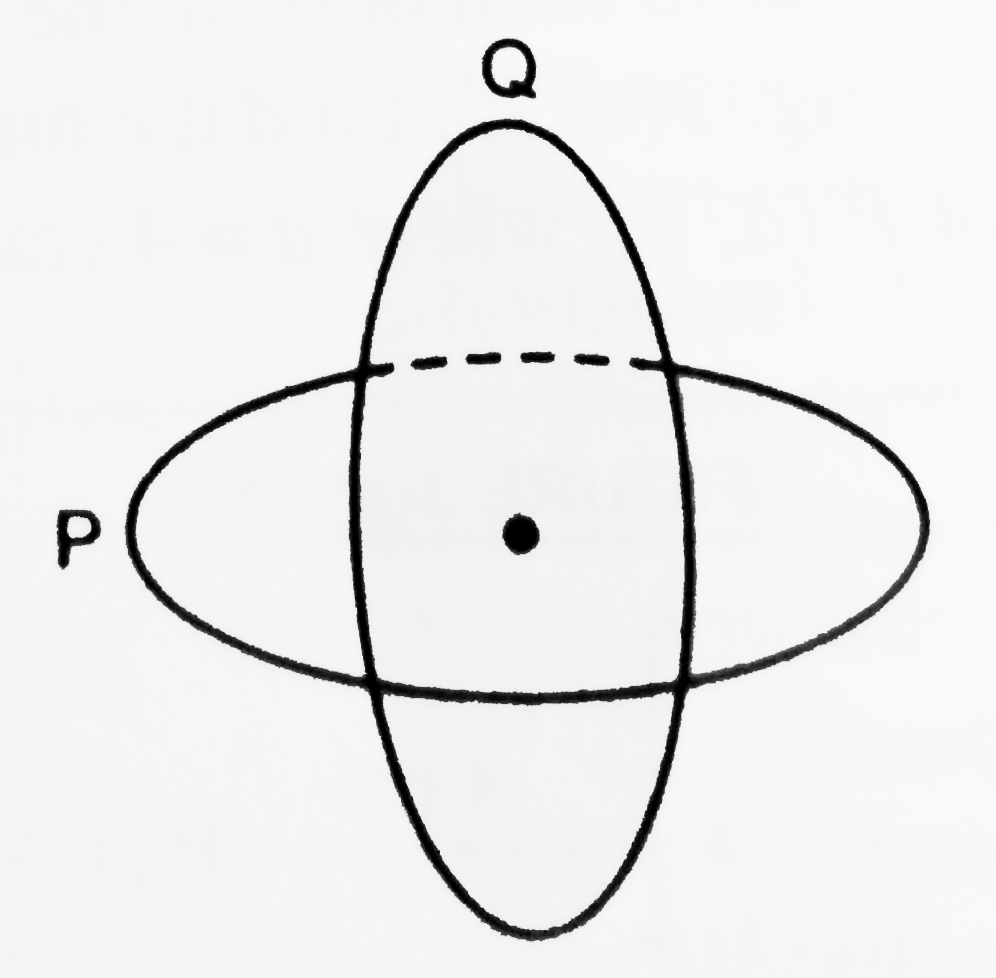
Two identical circular loops P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops is clockwise as seen from O which is equidistant from the both loops. Find the magnitude of the net magnetic field at point O.
So magnetic field at point O has a magnitude μ0I/4√2r
Related Solutions
Two identical circular loops, P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. Their centres are distance 2r apart. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O.
View SolutionTwo identical circular loops, P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. Their centres are distance 2r apart. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O.
View SolutionTwo identical circular loops, P and Q, each of radius r and carrying currents I and 2 I respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops in clockwise as seen from O, which is euqidistant from both loops. Find the magnitude of the net magnetic field at point O.

View Solutionदो समरूप (Identical) वृत्ताकार लूप P और Q जिनमें से प्रत्येक की त्रिज्या है तथा जिनमें क्रमशः I और 2I धाराएँ प्रवाहित हो रही हैं, एक-दूसरे के समांतर तल में इस प्रकार स्थित हैं कि उनका अक्ष उभयनिष्ठ है । दोनों लूपों से समान दूरी पर स्थित बिंदु 0 से देखे जाने पर दोनों में दक्षिणावर्त (Clockwise) दिशा में धारा प्रवाहित होती है। बिंदु O पर नेट चुंबकीय क्षेत्र का परिमाण ज्ञात कीजिए।
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
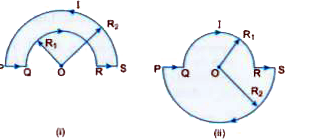
Determine the magnetic field at the centre point O due to two concentric semicircular loops of radii carrying a current I, when the loops of radii carrying a current I, when the loops are arranged as shown in Fig.
View SolutionTwo identical circular loops P and Q carrying equal currents are placed such that their geometrical axis are perpendicular to each other as shown in figure. And the direction of current appear’s anticlockwise as seen from point O which is equidistant from loop P and Q. Find the magnitude and direction of the net magnetic field produced at the p oint O. tan theta = (B_2)/(B_1)=1, theta = pi//4 .
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d . The loop and the wire are carrying the same current I . The current in the loop is in the counterclockwise direction if seen from above. (q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions. (r) There is no magnetic field at P . (s) The wires repel each other. (4) When d~~a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that case
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA circular loop which is in the form of a major arc of a constant magnetic field B is applied in the vertical direction such that the magnetic lines of forces go into the plane. If R is the radius of circle and it carries a current I in the clockwise direction, then the force on the loop will be
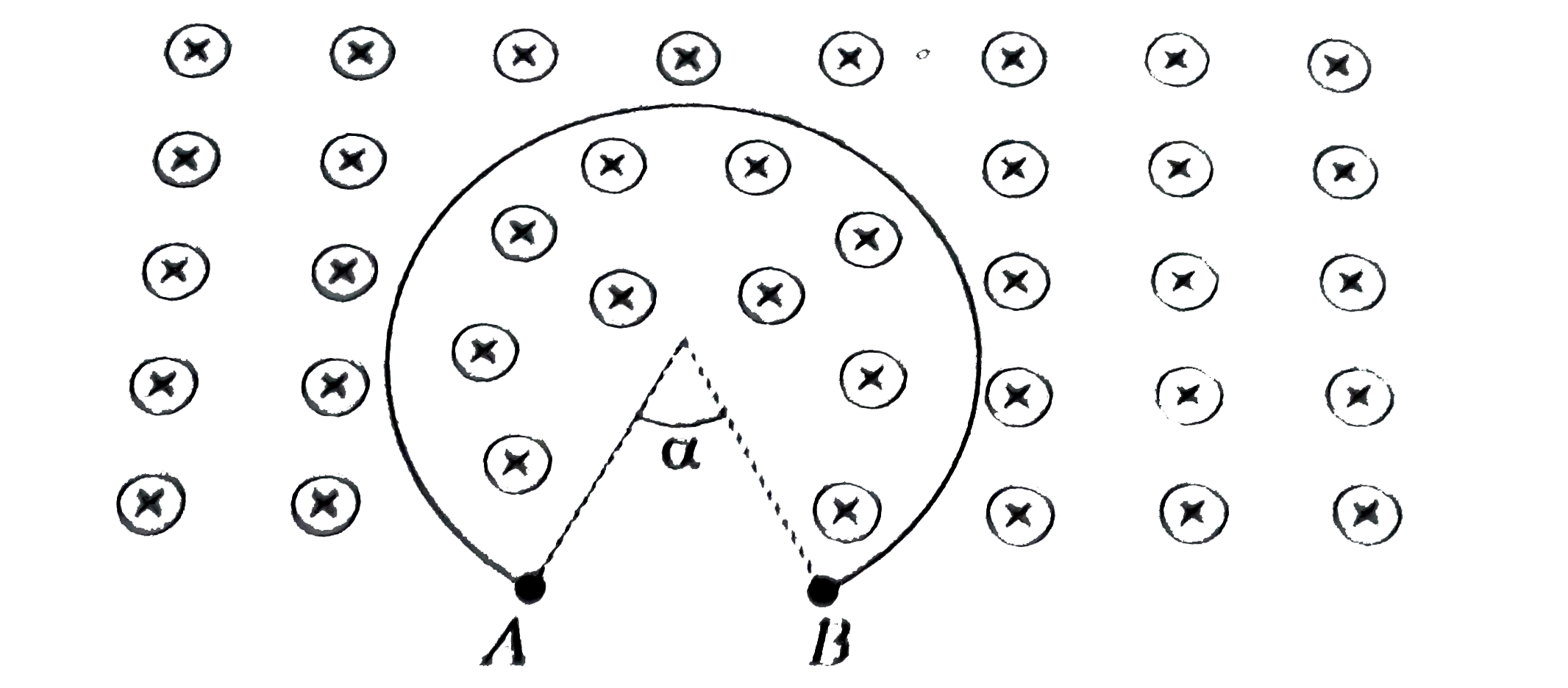
View SolutionA circular loop which is in the form of a major arc of a constant magnetic field B is applied in the vertical direction such that the magnetic lines of forces go into the plane. If R is the radius of circle and it carries a current I in the clockwise direction, then the force on the loop will be

View Solutionदो एकसमान समाक्ष वृत्ताकार लूपों में प्रत्येक में धारा I दक्षिणावर्त बह रही है। यदि लूप एक - दूसरे की ओर आ रहे हैं तो
View SolutionEach side of a hexagonal loop of a metal wire is a. The loop carries a current I. Find the magnitude of the magnetic field at the centre of the loop
View Solutionविद्युतवाही एक लूप (पाश) में दो एक समान अर्धवृत्ताकार भाग है। प्रत्येक की त्रिज्या R है। एक x-y समतल में और दूसरा x-z समतल में स्थित है। यदि लूपं (पाश) में विद्युत धारा i हो तो, उनके उभयनिष्ठ केन्द्र पर दोनों अर्धवृत्ताकार भागों के द्वारा उत्पन्न परिणामी चुम्बकीय क्षेत्र है
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d . The loop and the wire are carrying the same current I . The current in the loop is in the counterclockwise direction if seen from above. (q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions. (r) There is no magnetic field at P . (s) The wires repel each other. (4) When d~~a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d . The loop and the wire are carrying the same current I . The current in the loop is in the counterclockwise direction if seen from above. (q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions. (r) There is no magnetic field at P . (s) The wires repel each other. (4) When d~~a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that case
View SolutionA circular loop of wire is carrying a current I (as shown in the figure) o applying a uniform magnetic field inward perpendicular to the plane of the loop the loop
View SolutionWrite equation for magnetic dipole of current carrying circular loop at (i) at axis (ii) at plane of loop and at x distance from centre point of loop.
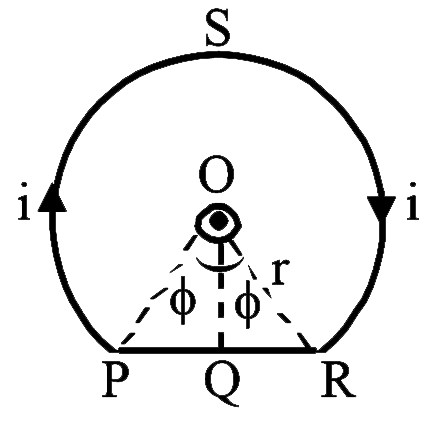
View SolutionConsider the loop PQRSP, carrying clockwise current i, shown in the figure. The magnitude of magnetic field at the centre O of the curved portion is
View SolutionTwo identical loops P and Q each of radius are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to and respectively.
View Solution