The point of intersection of the normals at A and B of a parabola y2 = 4ax meet on the line y = -a. Then the point of intersection of the tangents at A and B lies on the curvea xy = ab x2 = 4ayc xy = a2d x2 = 2ay
Correct option C xy = a2Explanation :Let A = at12 2at1 and B = at22 2at2 so that the point of intersection N of normals drawn at A and B isand lies on y = -a. This implies-at1t2t1 + t2 = -a= t1t2t1 + t2 = 1 .....1Let T x y be the intersection of the tangents at A and B. Hence x = at1t2 and y = at1 + t2. Therefore from Eq. 1 we getxy = at1 t2xa x t1 + t2 = a2
Related Solutions
. Find current enclosed in the loopMagnetic field at a point (x, y, z) is given by B- Boyix2 + y = 2(x2 + y2)2__Box(x2 + y2)2
View Solution3.(1) x + y = 0(2) x - y = 0If tangents are drawn from the origin to the curve y = sin x, then their points of contact lie on the curve(3) x2 - y2 = x2y2 (4) x2 + y2 = x2y2(2) x + y = xy(1) X- y = xy
View SolutionTangents are drawn to the parabola y^(2) = 4ax at the point where the line lx + my + n = 0 meet this parabola. Find the point of intersection of these tangents .
View SolutionNormal at the point A(2, -4) intersect the parabola y^(2)=8x at the point B. If the tangents at A and B meet at point R. If the area of DeltaABC is 16k, then k is _________.
View SolutionNormal at the point A(2, -4) intersect the parabola y^(2)=8x at the point B. If the tangents at A and B meet at point R. If the area of DeltaABC is 16k, then k is _________.
View SolutionTangents are drawn to the parabola at the point where the line meets this parabola. Find the point of intersection of these tangents.
View SolutionTangents at point B and C on the parabola intersect at A. The perpendiculars from points A, B and C to any other tangent of the parabola are in:
View SolutionTangents at point B and C on the parabola intersect at A. The perpendiculars from points A, B and C to any other tangent of the parabola are in:
View SolutionThe mid point of a variable chord AB of the parabola y^(2)=4ax lies on the line y=px where p is a constant,then find the equation of the locus of the points of intersection of the tangents at A and B.
View SolutionA tangent to the parabola y^(2)=4ax meets axes at A and B .Then the locus of mid-point of line AB is
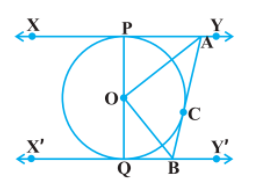
View Solutionदिये चित्र में, XY तथा X'Y' ,O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ है और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को Y तथा X' Y' को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि .

View Solutionदी गई आकृति में XY तथा X 'Y ', O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X 'Y ' को B पर प्रतिच्छेद करती है । सिद्ध कीजिए कि है ।
View SolutionIf parabola y^(2) = 4ax Points drawn on A and B. If the tangent lines meet at the point, then A, C and B. Have arms
View SolutionIn the xy-plane, the parabola with equation intersects the line with equation y = 25 at two points, A and B. What is the length of ?
View SolutionTangents are drawn at the end points of a normal chord of the parabola . The locus of their point of intersection is
View SolutionTangents are drawn at the end points of a normal chord of the parabola . The locus of their point of intersection is
View SolutionProve that BS is perpendicular to PS,where P lies on the parabola y^(2)=4ax and B is the point of intersection of tangent at P and directrix of the parabola.
View SolutionIf A is the mean of x,y and z and the additive inverse of (x+y)z is xy, then the mean of x2,y2 and z2 is
View SolutionThe line y=x-2 cuts the parabola y^(2)=8x in the points A and B. The normals drawn to the parabola at A and B intersect at G. A line passing through G intersects the parabola at right angles at the point C,and the tangents at A and B intersect at point T.
View SolutionThe ,locus of the point of intersection of two perpendicular tangents to the parabola y^(2)=4ax is
View Solution