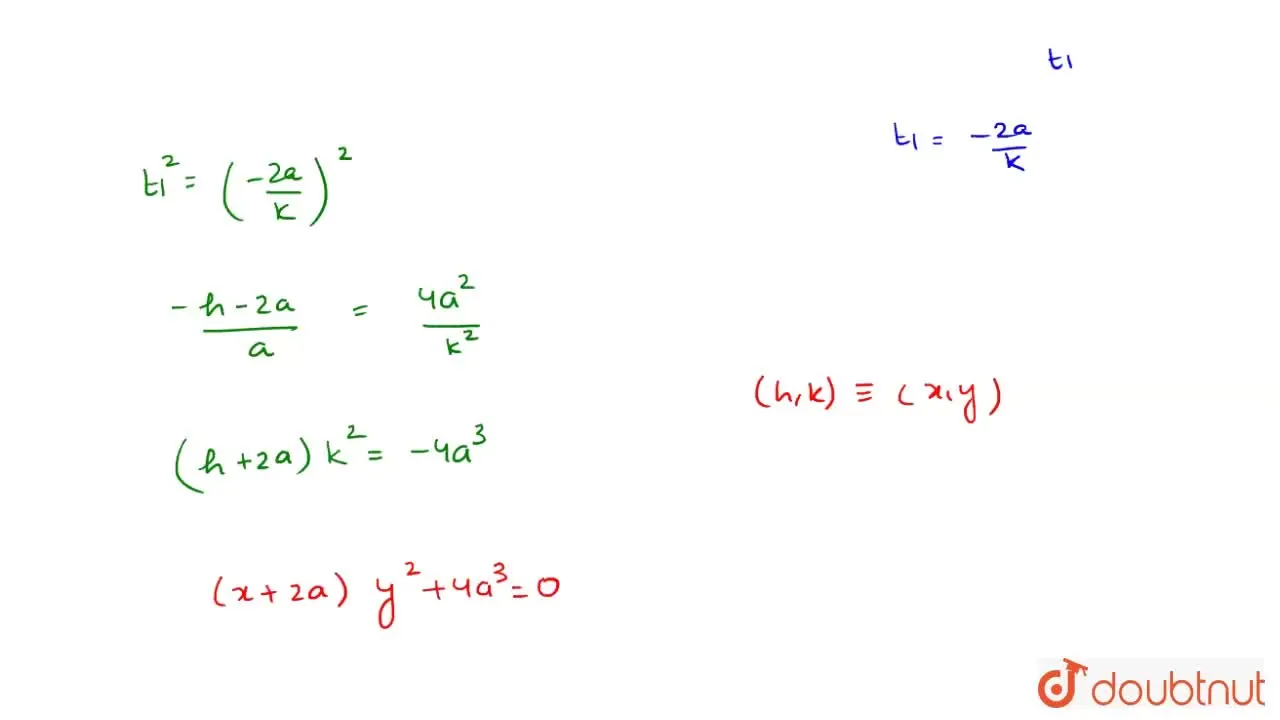Tangents are drawn at the end points of a normal chord of the parabola y2=4ax. The locus of their point of intersection is
(x−2a)y2+4a3=0
(x−2a)y2−4a3=0
(x+2a)y2−4a3=0
(x+2a)y2+4a3=0
The correct Answer is:D
Step by step video, text & image solution for Tangents are drawn at the end points of a normal chord of the parabola y^(2)=4ax. The locus of their point of intersection is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Find the locus of midpoint normal chord of the parabola y2=4ax
View SolutionThe locus of the middle points of normal chords of the parabola y2=4ax is-
View SolutionFind the locus of the midpoint of normal chord of parabola y2=4ax
View SolutionTangents are drawn at the ends of any focal chord of the parabola y2=16x. Then which of the following statements about the point of intersection of tangents is true.
View SolutionThe locus of the middle points of the normal chords of the parabola, y2=4ax is
View SolutionThe locus of the middle points of the focal chord of the parabola y2=4ax, is
View SolutionTangents are drawn from points of the parabola y2=4ax to the parabola y2=4b(x−c). Find the locus of the mid point of chord of contact.
View SolutionIf tangents be drawn from points on the line x=c to the parabola y2=4x, show that the locus of point of intersection of the corresponding normals is the parabola.
View SolutionThe tangents at the end points of any chord through (1,0) to the parabola y2+4x=8 intersect
View SolutionThe locus of the poles of the normal chords of the parabola y2=4ax is ..........
View Solution