Determine the support reaction and nature and magnitude of forces in members BC and EF of the diagonal truss shown in fig
First find the support reaction which can be determined by considering equilibrium of the truss. Let RAH & RAV be the support reaction at hinged support A and RDV be the support reaction at roller support D.∑H = 0RAH + 10 = 0RAH = – 10 KN∑V = 0RAV + RDV = 40 ...iTaking moment about point A ∑MA = 040 x 2 – 10 x 2 – RDV x 6 = 0RDV = 10KNFrom equation i; RAV = 30KN Let draw a section line 1-1 which cut the member BC EC FE and divides the truss in two parts RHS and LHS as shown in fig. Make the direction of forces only in those members which cut by the section line. i.e. in BC EF and EC Since the question ask the forces in the member BC and EF but by draw a section line member EC is also cut by the section line so we consider the force in the member EC.Choose any one part of them Since both parts are separately in equilibrium. Let we choose right hand side portion as shown in fig b. And the Right hand parts of truss is in equilibrium under the action of following force1. Reaction RDV = 10KN at the joint D2. 10KN load at joint F 3. Force TBC in member BC 4. Force TCE in member CE 5. Force TFE in member FEAll three forces are assumed to be tensileNow we take moment of all these five forces only from any point of the truss for getting the answers quicklyTaking moment about point C of all the five forces given above∑MC = 0Moment of Force TBC TCE about point C is zero since point C lies on the line of action of that forces– RD x CD + TEF x CF – 10x CF = 0–10 x 2 + TEF x 2 – 10x 2 = 0TEF = 20KNTEF = 20KN Tensile ...iiiTaking moment about point E of all the five forces given above ∑ME = 0Moment of Force TEF TEC and 10KN about point E is zero since point E lies on the line of action of that forces.– RD x BD – TBC x CF = 0–10 x 4 – TBC x 2 = 0TBC = –20KNTBC = 20KNCompressive.
Related Solutions
The cube as shown in Fig. 1.61, 75.0 cm on a side, is placed in a uniform magnetic field of 0.860 T parallel to the x-axis. The wire abcdef carries a current of 6.58 A in the direction indicated.
(a) Determine the magnitude and direction of the force acting on the segment ab.
(b) Determine the magnitude and direction of the force acting on the sement bc.
(c) Determine the magnitude and direction of the force acting on the segment cd.
(d) Determine the magnitude and direction of the force acting on the segment de.
(e) Determine the magnitude and direction of the force acting on the segment ef.
(f) What are the magnitude and direction of the total force on the wire ?

View SolutionThe cube as shown in Fig. 1.61, 75.0 cm on a side, is placed in a uniform magnetic field of 0.860 T parallel to the x-axis. The wire abcdef carries a current of 6.58 A in the direction indicated.
(a) Determine the magnitude and direction of the force acting on the segment ab.
(b) Determine the magnitude and direction of the force acting on the sement bc.
(c) Determine the magnitude and direction of the force acting on the segment cd.
(d) Determine the magnitude and direction of the force acting on the segment de.
(e) Determine the magnitude and direction of the force acting on the segment ef.
(f) What are the magnitude and direction of the total force on the wire ?

View SolutionDetermine the current in branches AB and BC of the network shown in Fig.
View SolutionIn fig. BA||ED and BC||EF. Show that angleABC=angleDEF
View SolutionIn fig. BA||ED and BC||EF> show that angleABC+angleDEF=180^@
View SolutionIn the fig. AB=EF, BC=DE, AB bot BD and EF bot CE . Prove that triangleABD equiv triangleFEC
View SolutionABCD ট্রাপিজিয়াম-এর দুটি তির্যক বাহু AD ও BC-এর মধ্যবিন্দু যথাক্রমে E ও F, প্রমাণ করো এবং ।
View SolutionThe path of particle is shown in figure. The ratio of distance travelled and magnitude of displacement is : EF=AB=2m FG =BC =2m CD=DE =1m
View SolutionIn the fig. show that AB||EF
View SolutionTwo dipoles are placed along the same axis at a distance x apart as shown in (Fig. 3.119). What is the magnitude of the force of interaction ? What is the nature of force, attractive or repulsive ?
 .
.
View SolutionTwo dipoles are placed along the same axis at a distance x apart as shown in (Fig. 3.119). What is the magnitude of the force of interaction ? What is the nature of force, attractive or repulsive ?
 .
.
View SolutionIn a trapezium ABCD, AB||DC and DC=2AB. EF drawn parallel to AB cuts AD in F and BC in E such that (BE)/(BC)=3/4 .Diagonals DB intersects EF at G. Prove that 7EF=10AB.
View SolutionABCD is a trapezium in which and AD = BC (See Fig.)
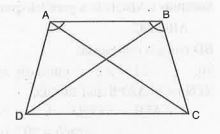 Show that diagonal AC = diagonal BD.
Show that diagonal AC = diagonal BD.
View SolutionABCD is a trapezium in which and AD = BC (See Fig.)
 Show that diagonal AC = diagonal BD.
Show that diagonal AC = diagonal BD.
View SolutionIn Fig. (ii), AD = BC and AD || BC. IS AB = DC? Give reasons in support of your answer.Hint. Prove that .
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
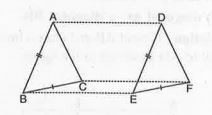 Show that quadrilateral ABED is a parallelogram.
Show that quadrilateral ABED is a parallelogram.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
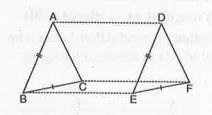 Show that .
Show that .
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral ABED is a parallelogram.
Show that quadrilateral ABED is a parallelogram.
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that .
Show that .
View SolutionIn and , AB = DE, , BC = EF and . Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that AC=DF.
Show that AC=DF.
View Solution