In Fig. (ii), AD = BC and AD || BC. IS AB = DC? Give reasons in support of your answer.Hint. Prove that △ABC=△CDA.
The correct Answer is:Yes
To determine whether AB is equal to DC given that AD = BC and AD || BC, we can use the properties of triangles and congruence. Here’s a step-by-step solution:
Step 1: Identify the triangles
We have two triangles: Triangle ABC and Triangle ADC.
Step 2: State the given information
We know that:
- AD = BC (given)
- AD || BC (given)
Step 3: Use the property of parallel lines
Since AD is parallel to BC, we can use the property of alternate interior angles. This means:
- Angle DAC = Angle ACB (alternate angles)
Step 4: Identify the corresponding angles
In triangles ABC and ADC, we can identify the angles:
- Angle ABC and Angle ADC are corresponding angles because they are both angles formed by the transversal AC intersecting the parallel lines AD and BC.
Step 5: Write down the angles
So we have:
- Angle DAC = Angle ACB (from step 3)
- Angle ABC = Angle ADC (corresponding angles)
Step 6: Conclude about the triangles
Now we have:
- AD = BC (given)
- Angle DAC = Angle ACB
- Angle ABC = Angle ADC
This means that the two triangles (ABC and ADC) have:
- One pair of equal sides (AD = BC)
- Two pairs of equal angles (Angle DAC = Angle ACB and Angle ABC = Angle ADC)
Step 7: Apply the criteria for triangle congruence
By the Angle-Side-Angle (ASA) criterion for triangle congruence, we can conclude that:
- Triangle ABC is congruent to Triangle ADC.
Step 8: State the conclusion
Since the triangles are congruent, their corresponding sides are equal. Therefore:
- AB = DC.
Final Answer
Yes, AB is equal to DC because Triangle ABC is congruent to Triangle ADC.
---
We have two triangles: Triangle ABC and Triangle ADC.
We know that:
- AD = BC (given)
- AD || BC (given)
Since AD is parallel to BC, we can use the property of alternate interior angles. This means:
- Angle DAC = Angle ACB (alternate angles)
In triangles ABC and ADC, we can identify the angles:
- Angle ABC and Angle ADC are corresponding angles because they are both angles formed by the transversal AC intersecting the parallel lines AD and BC.
So we have:
- Angle DAC = Angle ACB (from step 3)
- Angle ABC = Angle ADC (corresponding angles)
Now we have:
- AD = BC (given)
- Angle DAC = Angle ACB
- Angle ABC = Angle ADC
- One pair of equal sides (AD = BC)
- Two pairs of equal angles (Angle DAC = Angle ACB and Angle ABC = Angle ADC)
By the Angle-Side-Angle (ASA) criterion for triangle congruence, we can conclude that:
- Triangle ABC is congruent to Triangle ADC.
Since the triangles are congruent, their corresponding sides are equal. Therefore:
- AB = DC.
Yes, AB is equal to DC because Triangle ABC is congruent to Triangle ADC.
Topper's Solved these Questions
- CONGRUENCEBook:RS AGGARWALChapter:CONGRUENCEExercise:EXERCISE
Explore 18 Videos
- COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)Book:RS AGGARWALChapter:COLLECTION AND ORGANISATION OF DATA (MEAN, MEDIAN AND MODE)Exercise:EXERCISE 21C
Explore 5 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:TEST PAPER (True/False)
Explore 4 Videos
Similar Questions
Knowledge Check
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤ADIn ΔABC,IfAD⊥BC, then AB2+CD2 is equal to
A2BD2BBD2+AC2C2AC2DNone of these
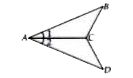
In the given figure, AB = AD and ∠1=∠2. Prove that : BC = DC
View SolutionIn a △ABC, AB = AC and AD⊥BC, then BD = .......
View SolutionIf AB∣∣DC and AD∣∣BC Find the value of x and y
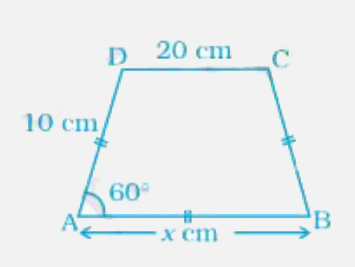
View SolutionIn the following figure, AB||DC and AD = BC. Find the value of x.
View SolutionIn ABC , if AD⊥BC and AD2=BD×DC , prove that ∠BAC=90o .
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View Solution


