A constant voltage is applied to a series R-L circuit at t = 0 by closing a switch. The voltage across L is 25V at t = 0 and drops to 5 V at t = 0.025 second. If L = 2H what must be the value of R ?
At t = 0 i = 0 hence there is no iR drop and the applied voltage must equal the back e.m.f. in the coil. Hence the voltage across L at t = 0 represents the applied voltage. At t = 0.025 second voltage across L is 5 V hence voltage across R = 25 − 5 = 20 V ∴ iR = 20 V − at t = 0.025 second. Now i = ImI − e −t/λ Here Im = 25/R ampere t = 0.025 second ∴ i = 25/R1 - e-0.025/λR x 25/R1 - e-0.0025/λ = 20 or e0.025/λ = 5∴ 0.025/λ = 2.3log105 = 1.6077∴ λ = 0.025/1.6077 Now λ = L/R = 2/R ∴ 2/R = 0.025/1.6077 ∴ R = 128.56 Ω
Related Solutions
A constant voltage is applied to a series R-L circuit by closing the switch. The voltage across inductor (L=2H) is 20V at t=0 and drops of 5V and 20 ms . The value of R in Omega is
View SolutionA constant voltage is applied to a series R-L circuit by closing the switch. The voltage across inductor (L=2H) is 20V at t=0 and drops of 5V and 20 ms . The value of R in Omega is
View SolutionA constant voltage of 25 V is applied to a series L-R circuit at t = 0 , by closing a switch . What is the pitential difference across the resister and the inductor at time t = 0?
View SolutionA constant voltage of 25 V is applied to a series L-R circuit at t = 0, by closing a switch. What is the potential difference across the resistor and the inductor at time t = 0?
View SolutionA constant voltage of 25 V is applied to a series L-R circuit at t = 0, by closing a switch. What is the potential difference across the resistor and the inductor at time t = 0?
View SolutionIn an L-C-R circuit, if V is the effective value of the applied voltage V_(R) is the voltage across R, V_(L) is the effective voltage across L, V_(C) is the effective voltage across C, then
View SolutionIn a L - C - R series AC circuit, the voltage across each of the component L, C and R is 50 V. The voltage across the L -R combination will be:
View SolutionAssertion :- Voltage across L (see figure) at t=0 is E Reason:- Because E=V_(L)+V_(R) and at t=0, i=0
View SolutionIn this R-L circuit, if the key is closed at , the time constant is
View SolutionSwitch is closed at then the current in the circuit at is
_PHY_E06_157_Q01.png)
View SolutionSwitch is closed at t = 0 then the current in the circuit at t = L/2R is
View SolutionIn an series circuit the voltages across and at resonance are 60V respectively the applied voltage is .
View SolutionIn the circuit given below, V(t) is the sinusoidal voltage source, voltage drop across the resistance R is
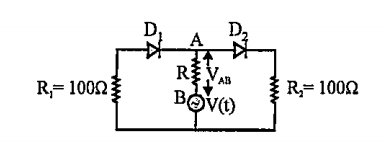
View SolutionIn the circuit given below , V(t) is the sinusoidal voltage source , voltage drop across the resistance R is
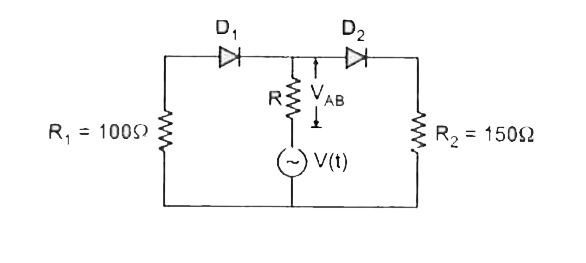
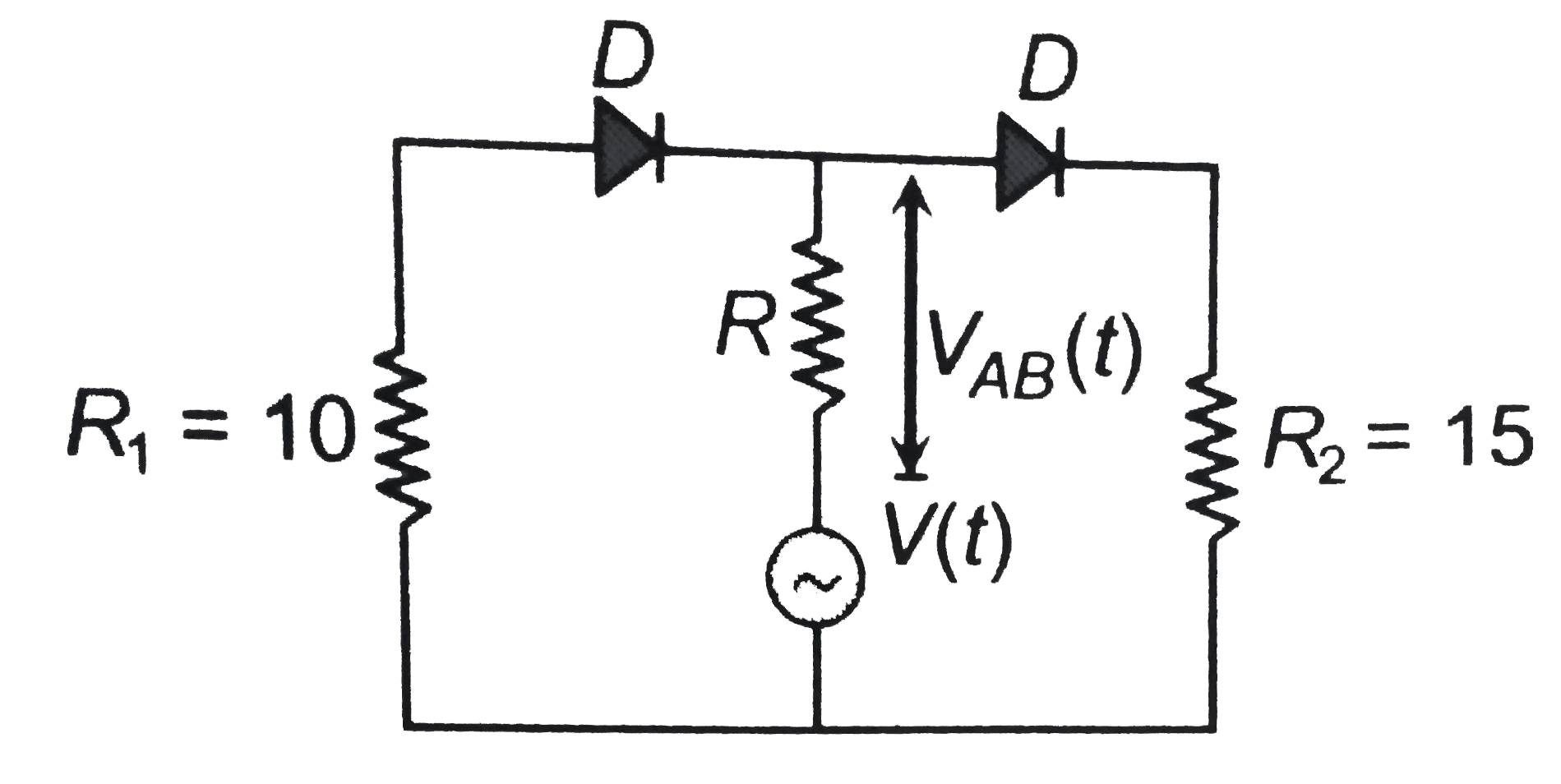
View SolutionIn the circuit given below, V(t) is the sinusoidal voltage source, voltage drop V_(AB)(t) across the resistance R is
View SolutionIn the circuit given below, is the sinusoidal voltage source, voltage drop across the resistance is
View SolutionAn AC circuit is consisting of a resistace R and an inductance L in series. The voltage across R is 60 V and the across L is 80 V. Find the total voltage across the combination. What is the phase difference between voltage and current?
View SolutionIn a L-C-R series A.C. circuit, the voltage across each of the components, L, C and R is 50V. The voltage across the L-C combination will be ......
View SolutionIn an LCR series circuit, the voltage across each of the components L,C,R is 20V. The voltage across the L-C combination will be:
View SolutionA time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)
View Solution