A machine of mass 75 kg is mounted on springs and is fitted with a dash pot to damp out vibrations there are three springs each of stiffness 10 n/mm and it is found that the amplitude of vibration diminishes from 38.4 mm to 6.4 mm in two complete oscillations. Assuming that the damping force varies as the velocity determine 1. The resistance of dash pot at unit velocity2. The ratio of frequency of the damped vibration to the un damped vibration3. The periodic time of the damped vibration.
m = 75 kg; s = 10 N/mm = 10 x 103 N/m; x1 = 38.4 mm = 0.0384 m; x3 = 6.4 mm = 0.00064 mSince the stiffness of each spring is 10 x 103 N/m and there are 3 springs therefore total stiffness s = 3 x 10 x 103 = 30 x 103 N/mWe know that natural circular frequency of motion Resistance of dash pot at unit velocityLet c = resistance of dash pot in newtons at unit velocity i.e. in N/m/s x2 = Amplitude after one complete oscillation in metres andx3 = Amplitude after two complete oscillation in metres.We know that x1/x2 = x2/x32. Ratio of frequency of the damped vibration to the un damped vibrationLet fn1 = frequency of the damped vibration = ωd/2πfn2 = frequency of the undamped vibration = ωn/2π3. Periodic time of the damped vibration.We know that periodic time of the damped vibration.
Related Solutions
A vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View SolutionA vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View SolutionA vibrating system consists of mass 12.5 kg, a spring of spring constant 1000 (N ) /( m ) performing damped oscillation with damping coefficient of 15 kg s^(-1) . The value of critical damping coefficient of the system is
View Solution(A) : In damped vibrations, Amplitude of oscillation decreases. (R): Damped vibrations indicate loss of energy due to air resistance
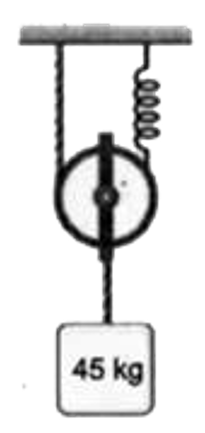
View SolutionThe system is released from rest with the spring initally stretched 75 mm . Calculate the velocity v of the block afrer it has dropped 12 mm . The spring has a stiffness of 1050 N//m . Neglect the mass of the small pulley.
View SolutionThe system is released from rest with the spring initially stretched 75 mm . Calculate the velocity v of the block after it has dropped 12 mm . The spring has a stiffness of 1050 N//m . Neglect the mass of the small pulley.
View SolutionThe system is released from rest with the spring initially stretched 75 mm. Calculate the velocity of the block after it has dropped 12 mm . The spring has a stiffness of 1050 Nm^(-1) . Neglect the mass of the small pulley.
View SolutionA 0.5 kg mass is suspended vertically from a point fixed on the Earth by a spring having a stiffness of 5 N/mm. What is its static displacement in (mm and m)? Solve by changing the unit into 'm' as well as 'mm'.
View SolutionA spring 40 mm long is stretched by the application of a force . If 10 N force required to stretch the spring through 40 mm is
View Solutionकिसी स्प्रिंग की लम्बाई 40 mm है। 10 N का बल लगाने से इसकी लम्बाई 1 मिमी बढ़ जाती है। स्प्रिंग को 40 मिमी खींचने में किया गया कार्य होगा :
View Solutionकम आयाम से कम्पन करती वस्तु पर कार्यरत - (i ) प्रत्यानयन बल , (ii ) अवमन्दन बल के मान क्या है ?
View SolutionA block of mass 0.1 kg is connected to an elastic spring of spring constant 640 Nm^(-1) and oscillates in a damping medium of damping constant 10^(-2) kg s^(-1) . The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to
View SolutionApplying force on the spring it stretches 40 mm. If a force of 10 N is required to pull 1 mm, then the work to be done to pull 40 mm .........
View SolutionA body of mass of 4 kg is mounted on four vertical springs each having a spring constant of 400 N/m. The period with which the body vibrates vertically is
View SolutionA LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring- mass damped oscillator having damping constant b, mass m and oscillating with a force constant k, the correct equivalence will be
View SolutionWhy does the amplitude of a vibrating body continuously decrease during damped vibrations ?
View Solutionचित्र में प्रदर्शित निकाय 75 मिमी खींची स्प्रिंग के साथ मुक्त किया जाता है| 12 मिमी गिरने के पश्चात ब्लॉक के वेग की गणना करें| स्प्रिंग का बल नियतांक 1050 न्यूटन/मी है| छोटी घिरनी का द्रव्यमान उपेक्षणीय है |
View Solutionअवमंदन बलो की उपस्थिति में पिंड का कंपन आयाम बढ़ता है।
View SolutionA 0.950 kg mass hangs vertically from a spring that he a spring constant of 8.50 N /m . The mass is set into vertical oscillations and after 600 s , you find tht the amplitude of the oscillation is That of initial amplitude.
What is the damping constant associated with this motion?
View Solution