A ball dropped from a point A falls down vertically to C through the midpoint B. The descending time from A to B and that from A to C are in the ratio a 1 : 1 b 1 : 2 c 1 : 3 d 1: √2
Correct option d 1: √2Explanation:For A to BS = 1/2gt2 ......iFor A to C2S = 1/2gt2 .....iiDividing i by ii we gett/t = 1/√2
Related Solutions
A ball dropped from a point A falls down vertically to C, through the midpoint B. The descending time from A to B and that from A to C are in the ratio
View SolutionA ball dropped from a point A falls down vertically to C, through the mid-point B. The descending time from A to B and that from A to C are in the ratio
View SolutionA body is falling freely from a point A at certain height from the ground and passes through point B, C and D (vertically as shown) so that BC=CD. The time taken by the particle to move from B to C is 2 seconds and from C to D 1 second. Time taken to move from A to B in second is
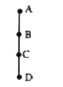
View SolutionA body is falling freely from a point A at certain height from the ground and passes through point B, C and D (vertically as shown) so that BC=CD. The time taken by the particle to move from B to C is 2 seconds and from C to D 1 second. Time taken to move from A to B in second is
View Solutionयदि चतुष्फलक OABC, जहाँ A, B, C क्रमशः (a, 2, 3), (1, b, 2) तथा (2, 1, c) से दिए जाते है, का केन्द्रक (1, 2, - 1) है, तो P(a, b, c) की मूल बिन्दु से दूरी है -
View SolutionIf the Point , where a,b,c are different from 1, lie on the line lx+my+n=0 then
View SolutionMatch the following and choose the correct combination from the options given : (a) {:(A, B, C, D),(3 , 1, 5, 4):} (b) {:(A, B, C, D),(1, 2, 3, 4):} (c) {:(A, B, C, D),(2, 1, 3, 4):} (d) {:(A, B, C, D),(3, 1, 5, 2):}
View Solutionयदि चतुष्फलक OABC, जहाँ A,B,C क्रमशः (a, 2, 3),(1, b, 2) व (2, 1, c) हैं, का केन्द्रक (1, 2, -1) है, तो बिन्दु P(a,b,c) की मूलबिन्दु से दूरी होगी
View SolutionProve that the points and are the vertices of a square .
View SolutionLet be two sets and let be a relation from A to B. Then is a relation from B to A.
View SolutionIf p is the length of perpendicular from the origin onto the plane whose intercepts on the axes area a,b,c then (A) (B) (C) (D) a^(-1)+b^(-1)+c^(-1)=1
View SolutionThe area of triangle formed by the vertices is (a) (b) (c) (d)
View SolutionMatch the following.

(A) 1-c, 2-b, 3-a
(B) 1-b, 2-c, 3-a
(C) 1-a, 2-b, 3-c
(D) 1-a, 2-c, 3-b
View SolutionIf , then what is the value of ? (a) 0 (b) 1 (c) 3 (d)
View SolutionIf the points ((a^(3))/(a-1),(a^(2)-3)/(a-1))((b^(3))/(b-1),(b^(2)-3)/(b-1)),((c^(3))/(c-1),(c^(2)-3)/(c-1)) are a!=1,b!=1,c!=1, then find the value of abc-(ab+bc+ca)+3(a+b+c)
View SolutionChoose the correct answer from the following :
The value of
View SolutionChoose the correct answer from the following :
The value of
View SolutionSelect and write the correct answer from the given alternatives in each of the following:If a!=b!=c!=0 such that |(a^3-1,b^3-1,c^3-1),(a,b,c),(a^2,b^2,c^2)|=0
View SolutionIf , then the value of is (b) or (c) (d)
View SolutionIf is equal to a. 1/2 b. 2 c. 1 d.
View Solution