A fine light string ABCDE whose extremity A is fixed has weights W1 and W2 attached to it at B and C. It passes round a small smooth peg at D carrying a weight of 40 N at the free end E as shown in fig. If in the position of equilibrium BC is horizontal and AB and CD makes 150° and 120° with BC find i Tension in the portion AB BC and CD of the string and ii Magnitude of W1 and W2.
First string ABCD is split in to two parts and consider the joints B and C separately LetT1 = Tension in String ABT2 = Tension in String BCT3 = Tension in String CDT4 = Tension in String DE T4 = T3 = 40 NSince at joint B and C three forces are acting on both points. But at B all three forces are unknown and at point C only two forces are unknown SO Apply lamis theorem first at joint C T2 /sin 150° = W2/sin 120° = 40/sin 90°= 20NT2 = {sin 150° × 40}/sin 90°W2 = {sin 120° × 40}/sin 90°= 34.64NNow for point B We know the value of T2 So Again Apply lamis theorem at joint B T1/sin 90° = W1/sin 150° = T2/sin 120°T1 = {sin 90° × 20}/sin 120° = 23.1 NW1 = {sin 150° × 20}/sin 120°= 11.55N
Related Solutions
Two uniform rods AB and BC of weight w per unit length hinged smoothly at B . They are kept in horizontal position with end A hinged smoothly at a fixed point and the rod BC resting on a peg D . If BD = k .BC , find the value of k in terms of AB and BC. Also find the reactions at A and D .
View SolutionAn L shaped uniform rod of mass 2M and length 2L (AB = BC = L) is held as shown in Fig. with a string fixed between C and wall so that AB is vertical and BC is horizontal. There is no friction between the hinge and the rod at A . If the string is burnt, find the angle between AB and the vertical at equilibrium position.
View SolutionAn shaped uniform rod of mass and length is held as shown in Fig. with a string fixed between and wall so that is vertical and is horizontal. There is no friction between the hinge and the rod at .

If the string is burnt, find the angle between and the vertical at equilibrium position.
View Solution20°C তাপমাত্রার জলে নিমজ্জিত অবস্থায় একটি কঠিন বস্তুখন্ডের আপাত ওজন W1। তাপমাত্রা বেড়ে 40°C হলে ওই আপাত ওজন হয় w2 । এক্ষেত্রে
View SolutionIn the given figure, ABCD is a trapezium with angle cm and cm. Find :
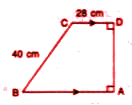
(i) AB
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
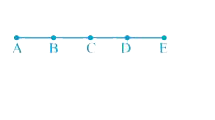
AD = AB + ________
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
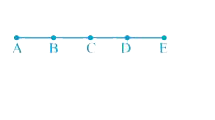
AE = ________ AB.
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights and ?
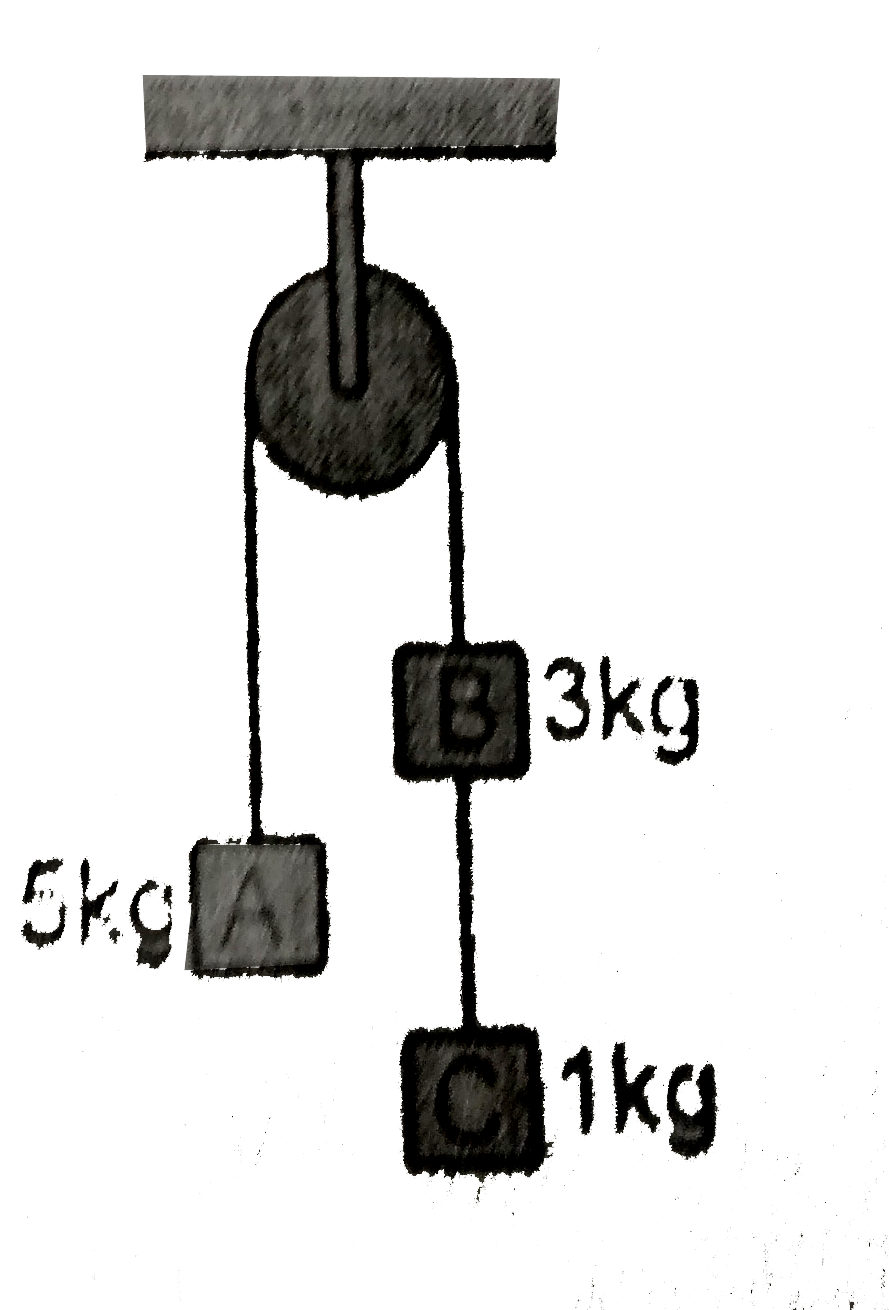
View SolutionThree weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights and ?
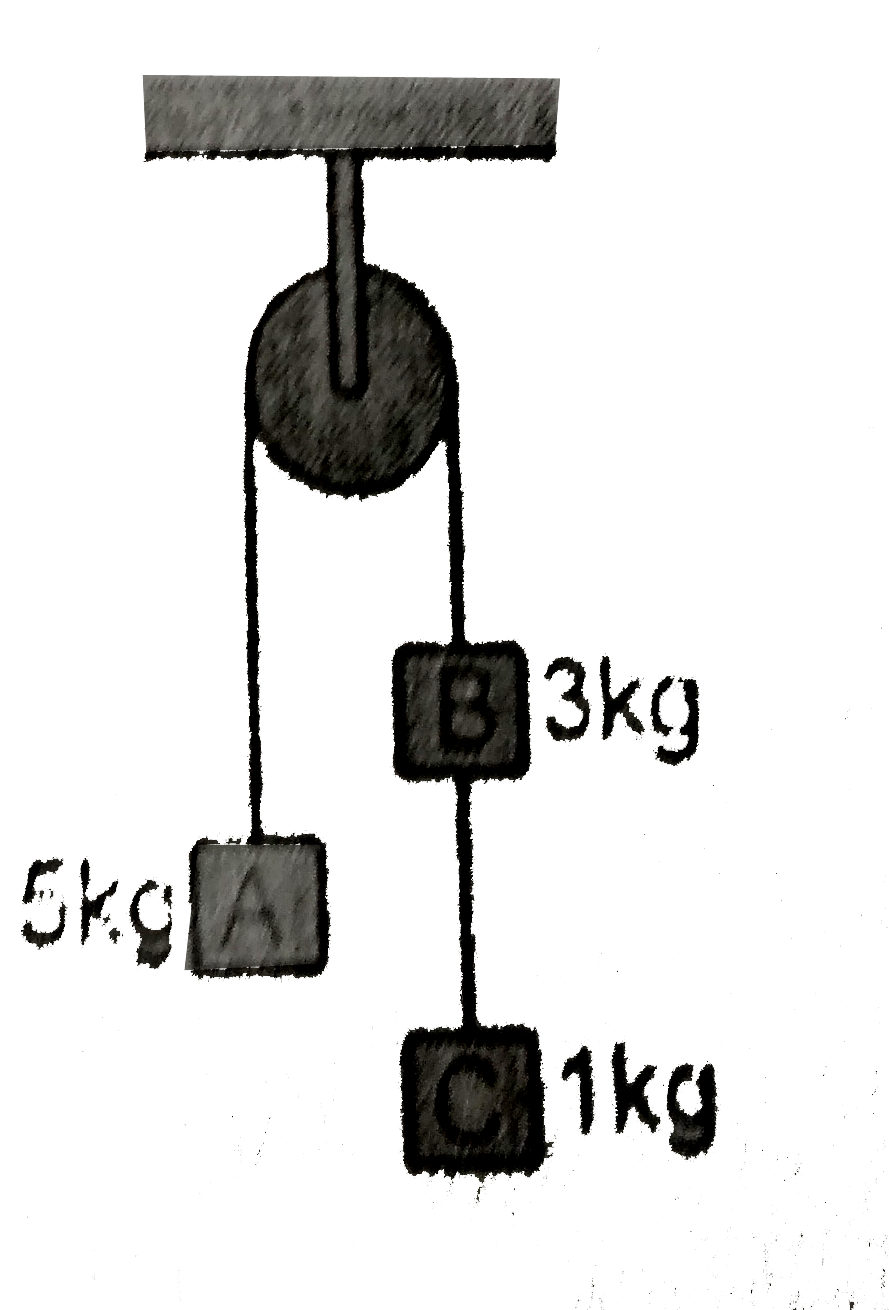
View SolutionA block of mass 'm' is attached to one end of a light inextensible string passing over a smooth light Pulley B and under another smooth light Pulley A as shown is figure. The other end of a string is fixed to a ceilling . A and B are held by springs of spring constant K_1 and K_2 . Find the angular frequency of small oscillation of the system
View SolutionFigure, represents a light inextensible string ABCDE in which and to which are attached masses M,m, and M at the point B,C and D, respectively. The system hangs freely in equilibrium with ends A and E of the string fixed in the same horizontal line. it is given that and . Then the tension in the string BC is
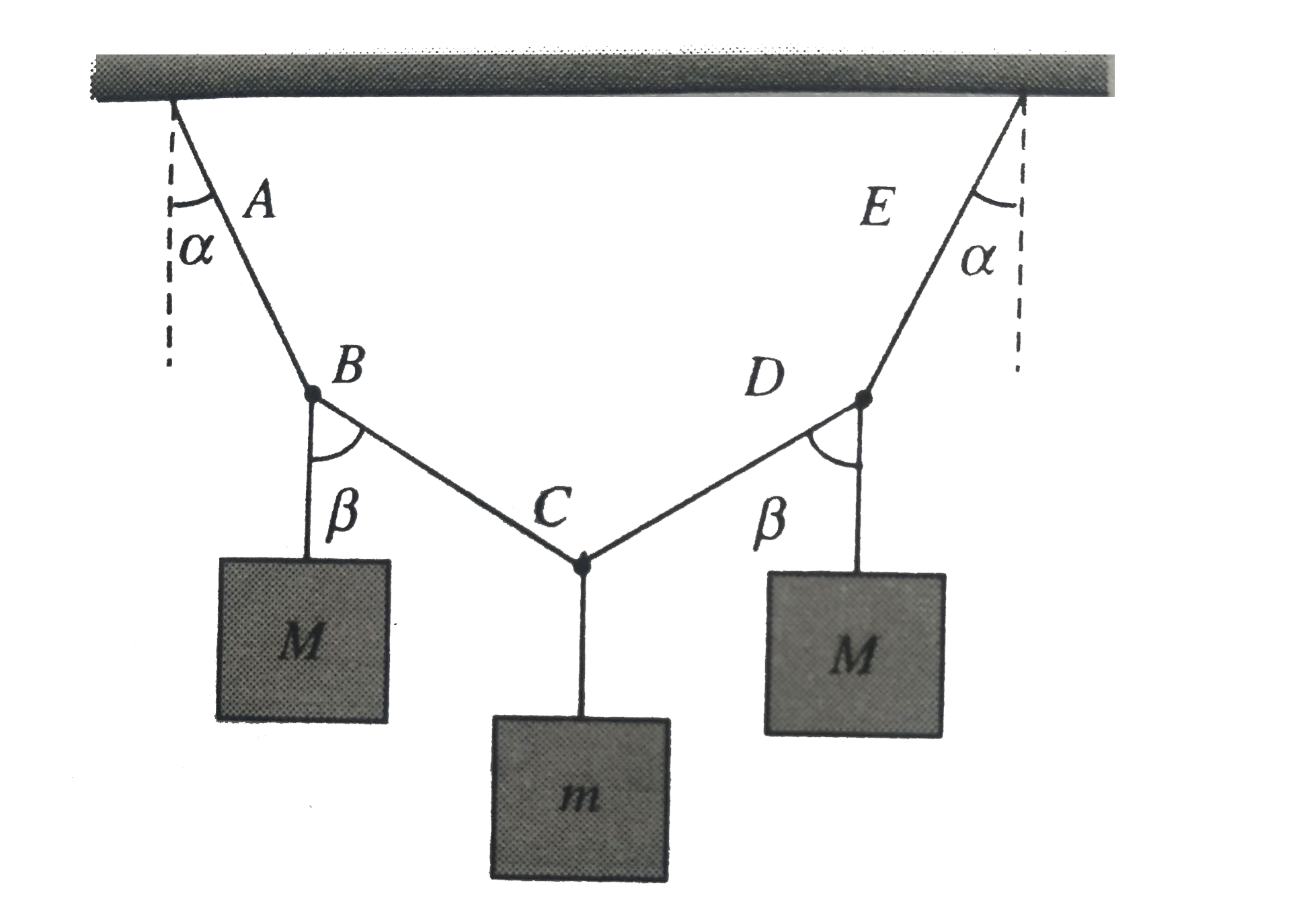
View SolutionFigure, represents a light inextensible string ABCDE in which and to which are attached masses M,m, and M at the point B,C and D, respectively. The system hangs freely in equilibrium with ends A and E of the string fixed in the same horizontal line. it is given that and . Then the tension in the string BC is

View SolutionA rigid bar AB is supported in a vertical plane and carries a load Q at its free end. Neglecting the weight of the bar, find the tension of the string CD.

View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
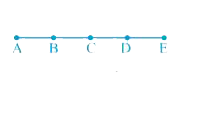
mid point of CE is __________
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
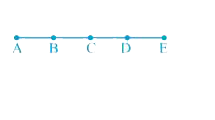
AD = AC + ___________
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
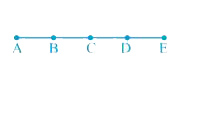
mid point of AE is __________
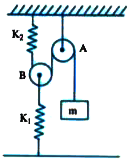
View SolutionA block of mass 'm' is tied to one end of string which passes over a smooth pulley 'A' and under a light smooth movable pulley B. The other end of the string is attached to lower end of a string constant . Find the period of small oscillations of mass 'm' about its equilibrium position.
View SolutionIf four sides of a quadrilateral are tangential to a circle, then (b) (c) (d)
View SolutionIf a, b, c, d are in H.P then ab + bc + cd =
View SolutionIn the quadrilateral ABCD, the circle is horizontal (see image) AB + CD = AD + BC.
View Solution