A rod of iron of Young’s modulus Y = 2.0 x 1011 N/m2 just fits the gap between two rigid supports 1m apart. If the rod is heated through 100°C the strain energy of the rod is α = 18 x 10-6 °C area of cross-section A = 1 cm2a 32.4 Jb 32.4 mJc 26.4 Jd 26.4 mJ
Correct option a 32.4 JExplanation:
Related Solutions
A elongation of 0.1% in a wire of cross-sectional area 10"6 m2 causes tension 100 N. The young’s modulus is
View SolutionA rod of length l made of isotropic material of Young's modulus Y, area of cross-section A is held between two rigid supports and heated uniformly. When the temperature is decreased by from , the tension will be
View SolutionA metallic rod breaks when strain produced is 0.2% . The Young's modulus of the material of the rod is 7xx10^(9)N//m^(2) . What should be its area of cross-section to support a load of 10^(4)N ?
View SolutionA metallic rod breaks when strain produced is 0.2% . The Young's modulus of the material of the rod is 7xx10^(9)N//m^(2) . What should be its area of cross-section to support a load of 10^(4)N ?
View SolutionA rod of 1m length and area of cross-section 1cm^(2) is connected across two heat reservoirs at temperature 100^(@)C and 0^(@)C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm^(-1)s^(-1)('^(@)C) ]
View SolutionThe temperature of an iron rod 0^circ C થી 100^circ C Longer than 1 m and 1 cm^2 How much force is generated in this cross-sectional rod? The rod is embedded at both ends. (α = 10^(-5)^circ C, Y = 10^(11) Pa) .
View SolutionA uniform rod of cross-section is heated from The coefficient of linear expansion of the rod, and Young's modulus The strain produced in the rod is
View SolutionA uniform rod of cross-section is heated from The coefficient of linear expansion of the rod, and Young's modulus The strain produced in the rod is
View SolutionAn aluminium rod has a breaking strain 0.2% . The minimum cross-sectional area of the rod in m^(2) in order to support a load of 10^(4)N is fi (Young's modulus is 7xx10^(9) Nm^(-2) )
View SolutionA uniform metal rod of 2mm^(2) area of cross section is heated from 0^(@)C to 20^(@)C . The coefficient of linear expansion of the rod is 12xx10^(-6)//""^(@)C . Its Young's modulus of elasticity is 10^(11)N//m^(2) , then the energy stored per unit volume of rod is,
View SolutionA uniform metal rod of 2mm^(2) area of cross section is heated from 0^(@)C to 20^(@)C . The coefficient of linear expansion of the rod is 12xx10^(-6)//""^(@)C . Its Young's modulus of elasticity is 10^(11)N//m^(2) , then the energy stored per unit volume of rod is,
View SolutionA rod of aluminium is fixed between two rigid support. If the temperature of rod is increased by , then the thermal stress on the rod is (Take Y=Pa and =2.4*)
View SolutionA rod of aluminium is fixed between two rigid support. If the temperature of rod is increased by 10°C , then the thermal stress on the rod is (Take Y= 7×10^10 Pa and alpha =2.4* 10^-5 K^-1 )
View SolutionPassage - II:
A copper rod of length and a steel rod of length , both having the same area of cross-section, are placed end to end between two rigid supports X and Y such that their system just fits between the supports with no initial stress in the rods. Temperature of the rods is now increased by . If is the Young's modulus of copper and its coefficient of linear expansion, while is the Young's modulus of steel and its coefficient of linear expansion, answer the following questions. (Assume that area of cross-section does not change and the rods do not bend. Also assume that there is no deformation of the supports.)
As the temperature is increased
View SolutionPassage - II:
A copper rod of length and a steel rod of length , both having the same area of cross-section, are placed end to end between two rigid supports X and Y such that their system just fits between the supports with no initial stress in the rods. Temperature of the rods is now increased by . If is the Young's modulus of copper and its coefficient of linear expansion, while is the Young's modulus of steel and its coefficient of linear expansion, answer the following questions. (Assume that area of cross-section does not change and the rods do not bend. Also assume that there is no deformation of the supports.)
As the temperature is increased
View SolutionA metal bar of length and area of cross-section A is clamped between two rigid supports. For the material of the rod. It Young's modulus is T and Coefficient if linear expansion is . If the temperature of the rod is increased by , the force exerted by the rod on the supports is
View SolutionA steel rod 2.0 m long has a cross-sectional area of 0.30cm^(2) . The rod is now hung by one end from a support structure, and a 550 kg milling machine is hung from the strain, and the elongation of the rod.
View SolutionA steel rod 2.0 m long has a cross-sectional area of . The rod is now hung by one end from a support structure, and a 550 kg milling machine is hung from the strain, and the elongation of the rod.
View SolutionAn aluminium rod has a breaking strain 0.2%. The minimum cross-sectional area of the rod in m^2 in order to support a load of 10^4N is if Youngs modulus is 7 xx 10^9 Nm^(-2)
View SolutionA rod of 1 m length and area of cross-section is connected across two heat reservoirs at temperatures as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod = 0.09 kilocal
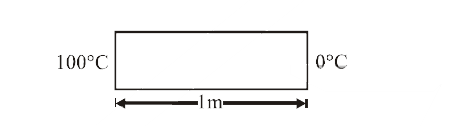
View Solution