A rod of 1m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperature 100∘C and 0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm−1s−1('∘C)]
![A rod of 1m length and area of cross-section 1cm^(2) is connected across two heat reservoirs at temperature 100^(@)C and 0^(@)C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod =0.09kilocalm^(-1)s^(-1)('^(@)C)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_HT_E01_049_Q01.png)
9×10−4kilocal/sec
9kilocal/sec
0.09kilocal/sec
9×10−6kilocal/sec
i=kAΔTl=0.09×1×10−4×1001
i=9×10−4kcal/sec
Topper's Solved these Questions
Similar Questions
A rod of 1 m length and area of cross-section 1cm2 is connected across two heat reservoirs at temperatures 100∘Cand0∘C as shown. The heat flow per second through the rod in steady state will be [Thermal conductivity of material of rod = 0.09 kilocal m−1s−1(∘C)]

View SolutionAn aluminium rod and a copper rod of equal length 1.0m and cross-sectional area. 1cm2 are welded together as shown in figure. One end is kept at a temperature of 20∘C and the other at 60∘C Calculate the amount of heat taken out per second from the hot end. thermal conuctivity of aluminium =200Wm−1^(@)C^(-1)andofcopper=390Wm^(-1)^(∘)C−1 .

View Solution
Knowledge Check
One end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
A3×103JB6×103JC9×103JD12×103JTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oilThe heat is flowing through a rod of length 50 cm and area of cross-section 5cm2 . Its ends are respectively at 25∘C and 125∘C . The coefficient of thermal conductivity of the material of the rod is 0.092kcal/m×s×.∘C . The temperature gradient in the rod is
A2∘C/cmB2∘C/mC20∘C/mD20∘C/cm
The ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionThree copper rods and three steel rods each of length l=10cm and area of cross-section 1cm2 are connected as shown

If ends A and E are maintained at temperatures 125∘C and 0∘C respectively, calculate the amount of heat flowing per second from the hot of cold function. [KCu=400W/m−K,Ksteel=50W/m−K]
View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
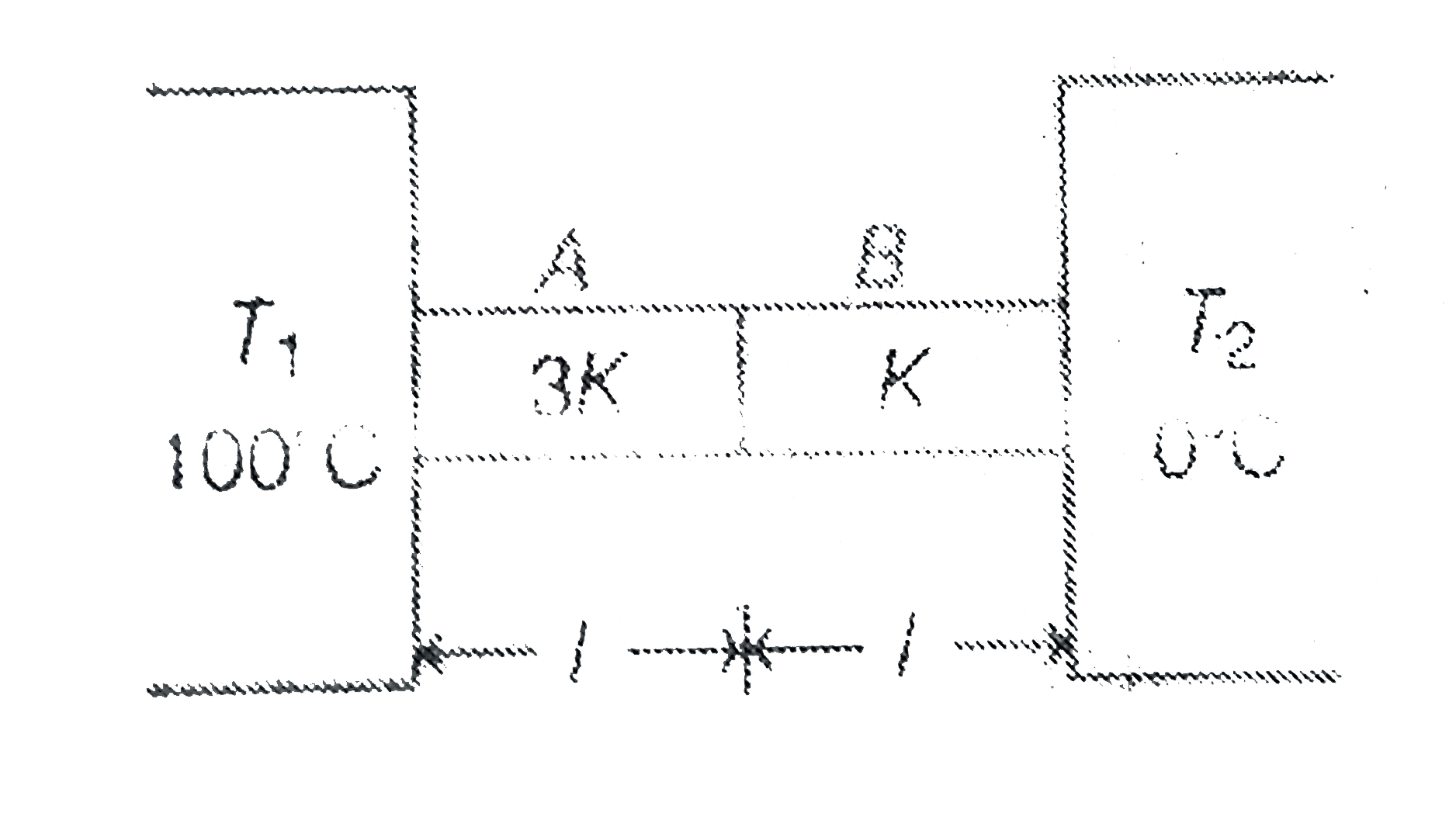
The ratio of the thermal resistance of the rods is
View Solution
